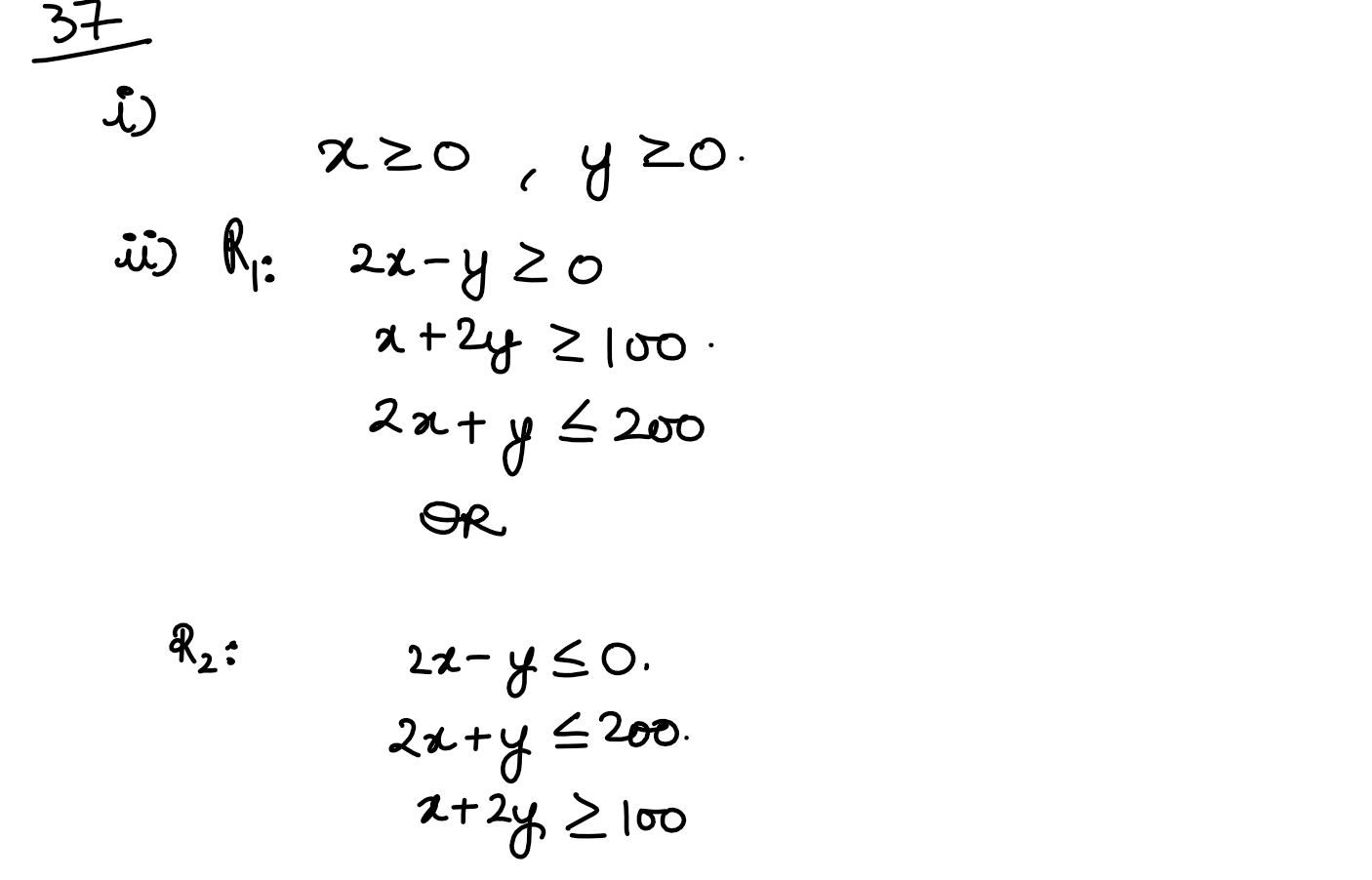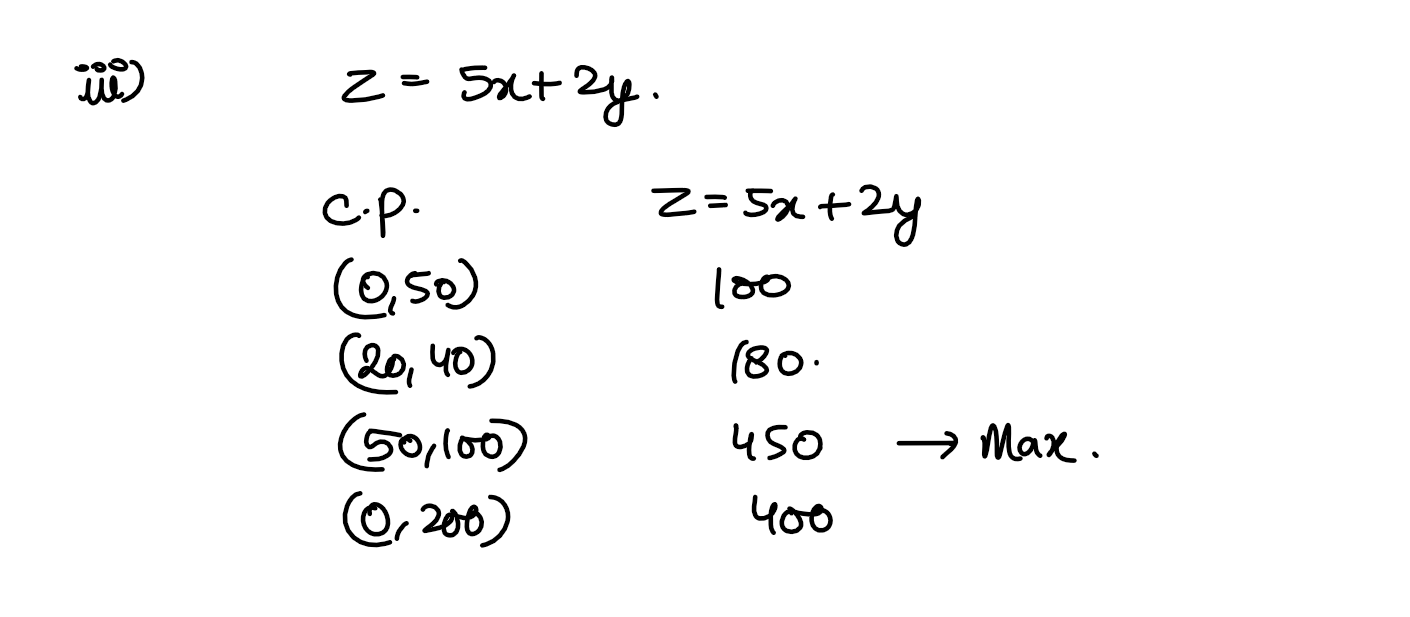Q37. Case Study — 2

In number theory, it is often important to find factors of an integer N. The number N has two trivial factors, namely I and N. Any other factor, if exists, is called non-trivial factor of N. Narcsh has plotted a graph of some constraints (linear inequations) with points A (0, 50), B (20 40), C(50, 100), D(O, 200) and E(IOO, 0). This graph is constructed using three non-trivial constraints and two trivial constraints. One of the non-trivial constraints is x + 2y ≥100



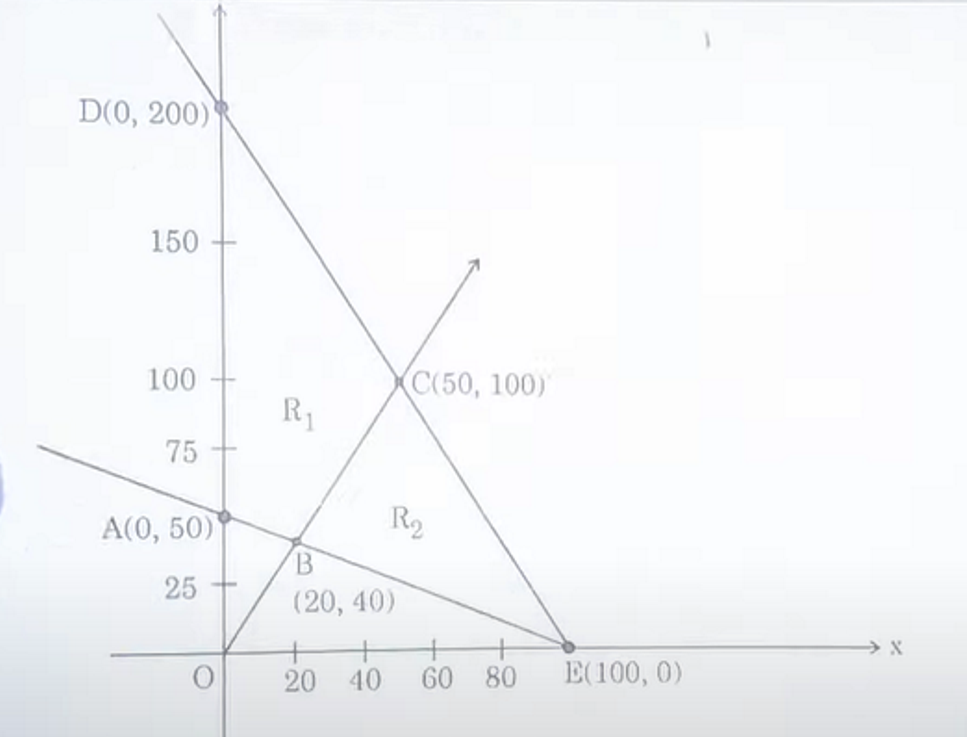
Based on the above information, answer the following questions

(i) What are the two trivial constraints ? (ii) (a) If R₁ is the feasible region, then what are the other two non-trivial constraints?

(b) If R₂ is the feasible region, then what are the other two non-trivial constraints ?

(iii) If R₁ is the feasible region, then find the maximum value of the objective function z = 5x + 2y.

Solution