Class 12 CBSE Question Paper 2023

Class 12 CBSE Applied Maths aims to develop an understanding of basic mathematical and statistical tools and their applications in the field of commerce (business/ finance/economics) and social sciences. Topics covered in Class 12th Applied Maths includes : Numbers, Quantification and Numerical Applications, Algebra, Calculus, Probability Distributions , Inferential Statistics, Index Numbers and Time-based data , Financial Mathematics , Linear Programming.


SECTION – A


Q1. The last (unit) digit of (22)12 is:
(a) 2
(b) 4
(c) 6
(d) 8

Solution :



Q2. The least non-negative remainder, when 315 is divided by 7 is:
(a) 1
(b) 5
(c) 6
(d) 7

Solution :



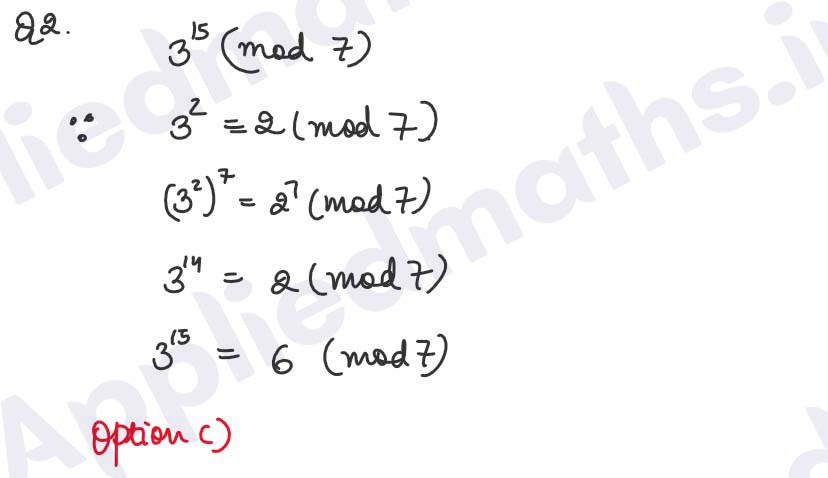
Q3.

Solution :



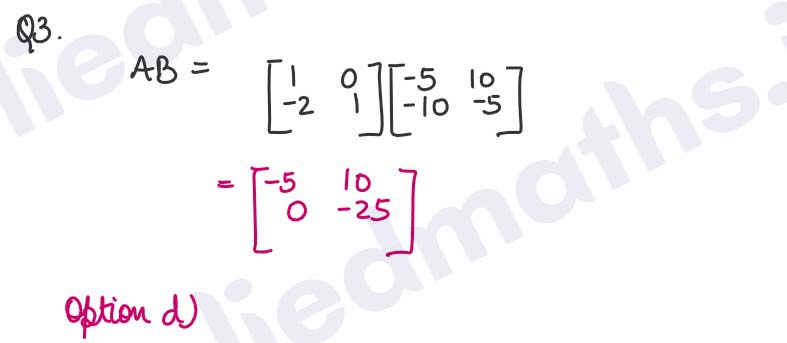
Q4.

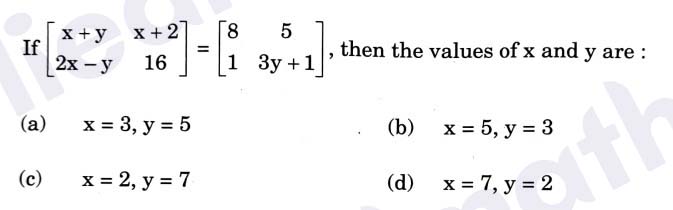
Solution :



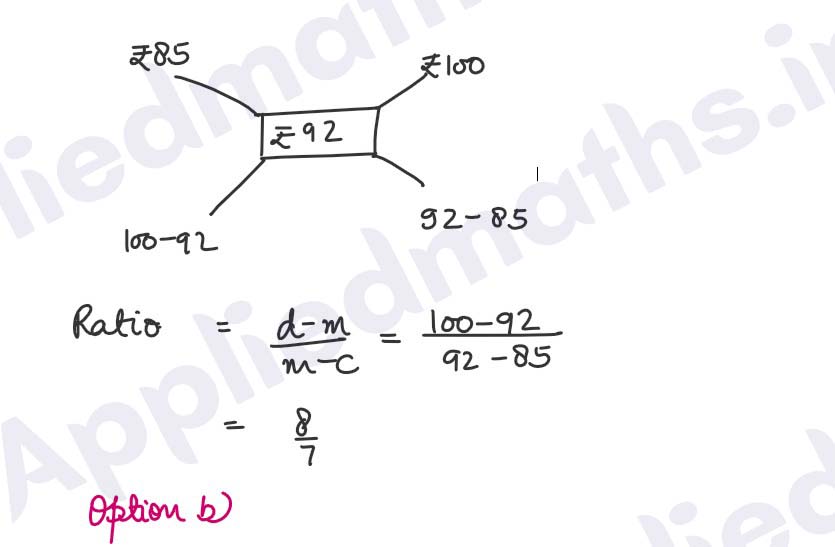
Q5. The ratio in which a grocer mixes two varieties of pulses costing Rs 85 per kg and Rs 100 per kg respectively so as to get a mixture worth Rs 92 per kg, is
(a) 7:8
(b) 8:7
(c) 5:7
(d) 7:5

Solution :



Q6.

Solution :



Q7. A and B are Square matrices each of order 3 such that |A| = - 1 and |B| = 3. What is the value of |3AB|?
(a) -9
(b) 18
(c) -27
(d)-81

Solution :



Q8.

Solution :



Q9.

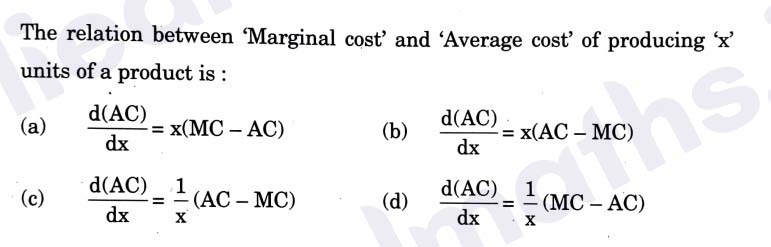
Solution :



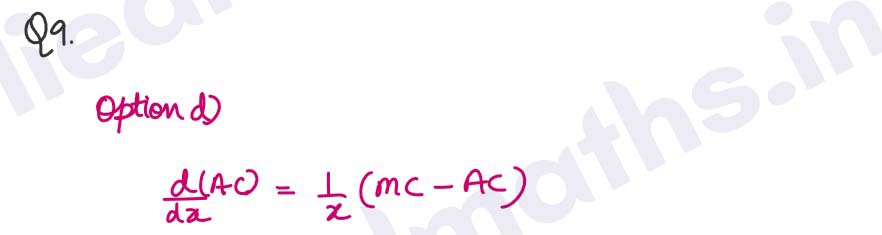
Q10.

Solution :



Q11.

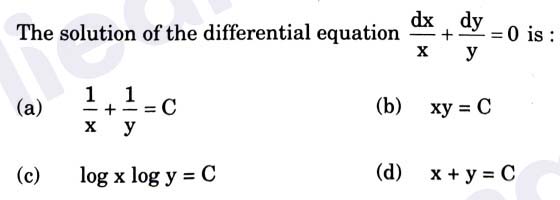
Solution :



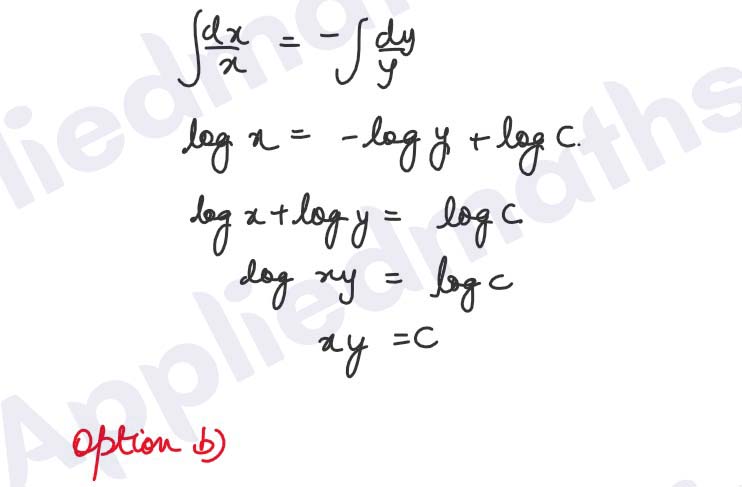
Q12. If X is a Poisson variable such that P(X = 1) = 2P(X = 2), then P(X = 0) is
(a) e
(b) 1/e
(c) 1
(d) e2

Solution :



Q13. If the calculated value of |t| < tv(α), then the null hypothesis is
(a) rejected
(b) accepted
(c) cannot be determined
(d) neither accepted nor rejected

Solution :



Q14.

Solution :



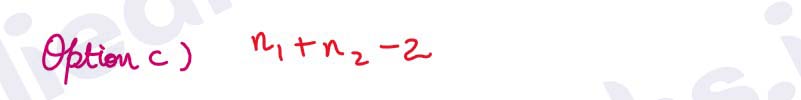
Q15.

Solution :



Q16.

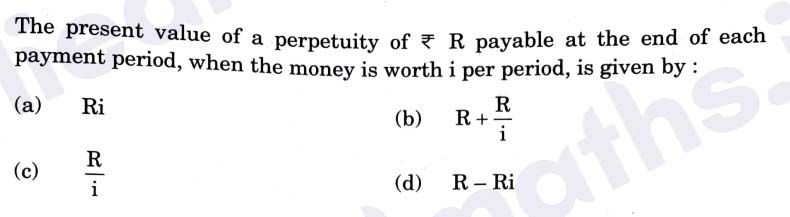
Solution :



Q17. The effective rate which is equivalent to nominal rate of 10% p.a: compounded quarterly is
(a) 10.25%
(b) 10.38%
(c) 10.47%
(d) 10.53%

Solution :



Q18. Region represented by x≥0, y≥0 lies in
(a) I quadran
t (b) II quadrant
(c) III quadrant
(d) IV quadrant

Solution :


For questions 19 and 20, two statements are given – one labelled Assertion(A) and the other labelled Reason (R). Select the correct answer to these questions from the codes (i), (ii), (iii) and (iv) as given below:

(i) Both A and R are true and R is the correct explanation of the assertion
(ii) Both A and R are true but R is not the correct explanation of the assertion
(iii) A is true, but R is false
(iv) A is false, but R is true


Q19.

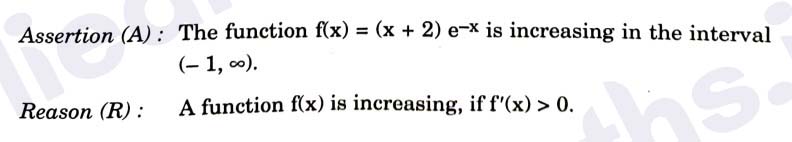
Solution :



Q20.

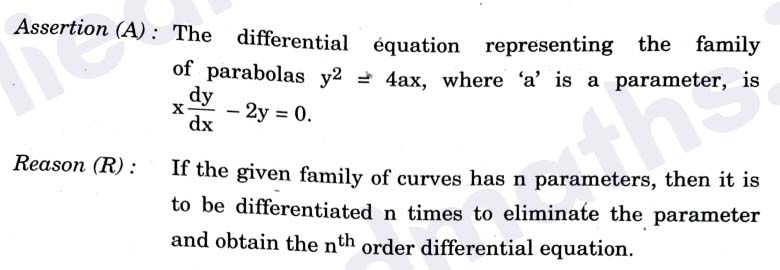
Solution :


SECTION – B


Q21. (a) Two pipes A and B can fill a tank in 24 minutes and 32 minutes 21. respectively. If both the pipes are opened simultaneously, after how much time should B be closed so that the tank is full in 18 minutes?
OR
(b) In a one-kilometre race, A beats B by 30 seconds andB beats C by 15 seconds. If A beats C by 180 metres, then find the time taken by A to run 1 kilometre

Solution :



Q22.

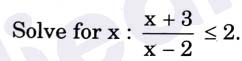
Solution :



Q23.

Solution :



Q24. A particle moves along the curve 6y = x3 + 2. Find the points on the curve at which the ordinate is changing 8 times as fast as abscissa

Solution :



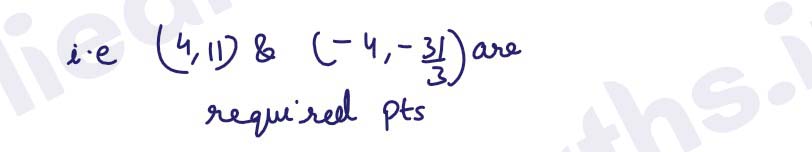
Q25. Suppose 2% of the items made by a factory are defective. Find thee probability that there are 3 defective items in a sample of 100 items selected at random. [Given e-2 = 0.135]

Solution :


SECTION-C


Q26. (a) A bottle is full of dettol. One-third of its dettol is taken away and an equal amount of water is poured into the bottle to fill it again. This operation is repeated three times. Find the final ratio of dettol to water in the bottle.
OR
(b) A pipe A can fill a tank in 3 hours. There are two outlet pipes B and C from the tank which can empty it in 7 and 10 hours respectively. It all the three pipes are opened simultaneously, how long will it take to fill the tank ?

Solution :



Q27. Find all the points of local maxima and local minima for the function f(x) = x3-6x2 + 9x-8.

Solution :



Q28. An unbiased die is thrown again and again until three sixes are obtained. Find the probability of obtaining a third six in the sixth throw of the die.

Solution :



Q29. The mean weekly sales of a four-wheeler were 50 units per agency in 20 agencies. After an advertising campaign, the mean weekly sales increased to 55 units per agency with standard deviation of 10 units. Test whether the advertising campaign was successful
(Use t0.005 1.729 for 19 d.f.)

Solution :



Q30. (a) An asset costs Rs 4,50.000 with an estimated useful life of 5 years and a scrap value of Rs 1,00,000. Using linear depreciation method, nnd the annual depreciation of the asset and construct a yearly depreciation schedule.
OR
(b) Amrita bought a car worth Rs 12,50,000 and makes a down payment of Rs 3,00,000. The balance amount is to be paid in 4 years by equal monthly instalments at an interest rate of 15% p.a. Find the EMI that Amrita has to pay for the car.
{Given (1.0125)43 = 0.5508565}

Solution :



Q31.

Solution :


SECTION-D


Q32.

Solution :

Q33.(a) Divide a number 15 into two parts such that the square of one part multiplied with the cube of the other part is maximum.
OR
(b) Find a point on the curve y2 = 2x which is nearest to the point (1, 4)

Solution :



Q34. Fit a straight line trend by method of least squares to the following data and find the trend values

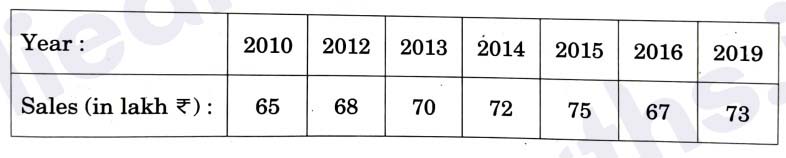
Solution :



Q35. Define Compound Annual Growth Rate (CAGR) and give the formula for calculating CAGR. Using the formula, calculate CAGR of Vikas's investment given below:
Vikas invested Rs 10,000 in a stock of a company for 6 years. The value of his investment at the end of each year is given below

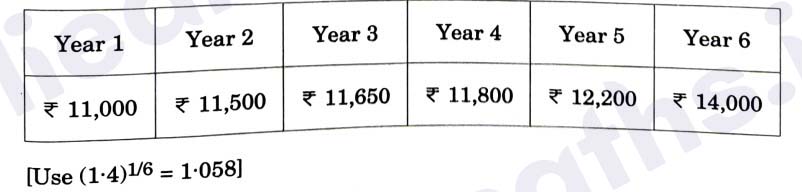
Solution :





SECTION-E


CASE STUDY – I

Q36. A factory produces bulbs, of which 6% are defective bulbs in a large Du of bulbs.
Based on the above information, answer the following questions (i) Fnd the probability that in a sample of 100 bulbs selected at random, none of the bulbs is defective. (Use:e-6 = 0.0024)
(ii) Find the probability that the sample of 100 bulbs has exactly two defective bulbs
(iii) (a) Find the probability that the sample of 100 bulbs will include not more than one defective bulb.
OR
(iii) (b) Find the mean and the variance of the distribution of number of defective bulbs in a sample of 100 bulbs.

Solution :



CASE STUDY – II

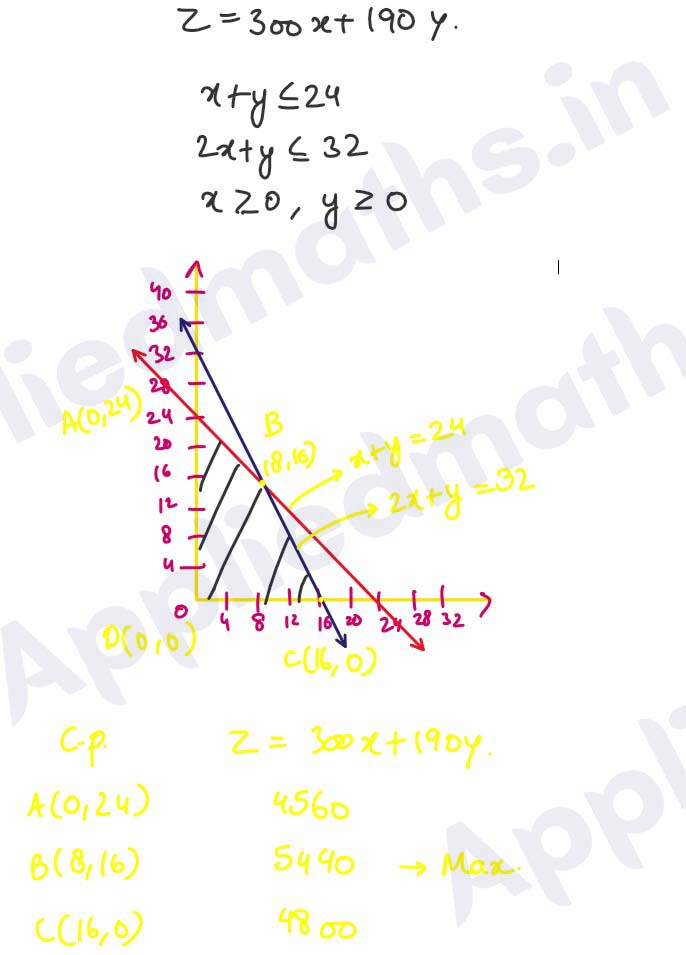
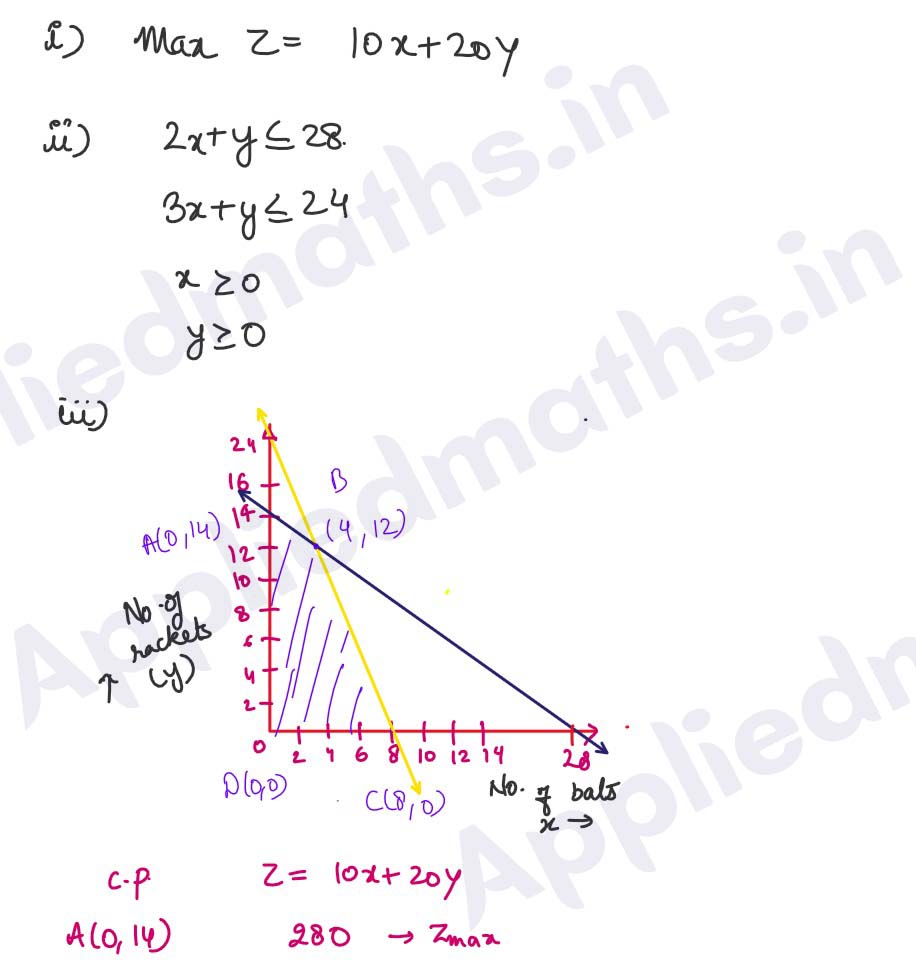
Q37. A factory manufactures tennis rackets and cricket bats. A tennis racket takes 1 (1/2) hours of machine time and 3 hours of craftsmanship in its making; while a cricket bat takes 3 hours of machine time and 1 hour of craftsmanship. In a day, the factory has availability of not more than 42 hours of machine time and 24 hours of craftsmanship. Profit on a racket and on a bat are Rs 20 and Rs 10 respectively.
Based on the above information, answer the following questions:
(i) If x and y are the numbers of bats and rackets manufactured by the factory, then write the expression of total profit.
(ii) Write the constraint that relates the number of craftsmanship hours.
(iii) (a) Determine the maximum profit (in Rs ) earned by the factory.
OR
(iii) How many bats and rackets respectively, are to be manufactured to earn maximum profit ?

Solution :



CASE STUDY – III

Q38. In the year 2010, Mr. Aggarwal took a home loan of Rs 30,00,000 from State Bank of India at 7.5% p.a. compounded monthly for 20 years.
Based on the above information, answer the following questions :
(i) Determine the EMI.
(ii) Find the principal paid by Mr. Aggarwal in the 150th instalment.
(iii) (a) Find the total interest paid by Mr. Aggarwal.
OR
(iii) (b) How much was paid by Mr. Aggarwal to repay the entire amount of home loan
[Use (1.00625)240 = 4.4608; (1.00625)91 = 1.7629]
Determine the trend of rainfall by three years moving average and draw the moving averages graph.

Solution :

Contact Us