Class 12 CBSE Specimen Paper 2024
Class 12 CBSE Applied Maths aims to develop an understanding of basic
mathematical and statistical tools and their
applications in the field of commerce (business/ finance/economics) and social
sciences. Topics covered in Class 12th Applied Maths includes : Numbers, Quantification and
Numerical Applications, Algebra, Calculus, Probability Distributions , Inferential Statistics, Index
Numbers and Time-based data , Financial Mathematics , Linear Programming.
SECTION – A
Q1. The value of -70 mod 13 is
(a) 5
(b) −5
(c) 8
(d)−8
Solution :

Q2. If 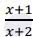 ≥ 1, then
(a) 𝑥 ∈ [−∞, 2] (b) 𝑥 ∈ (−∞, −2) (c) 𝑥 ∈ (−∞, 2] (d) 𝑥 ∈ (−∞, 2)
≥ 1, then
(a) 𝑥 ∈ [−∞, 2] (b) 𝑥 ∈ (−∞, −2) (c) 𝑥 ∈ (−∞, 2] (d) 𝑥 ∈ (−∞, 2)
Solution :

Q3. Which of the following is a statistic
(a) 𝜇
(b) 𝑥̅
(c) 𝜎2
(d) None
Solution :

Q4. In one sample t- test, the estimation for population mean is

Solution :

Q5. A man can row 6 km/h in still water. It takes him twice as long to row up as to row down the
river. Then the rate of the stream is
(a) 2 𝑘𝑚/ℎ
(b) 4 𝑘𝑚/ℎ
(c) 6 𝑘𝑚/ℎ
(d) 8 𝑘𝑚/ℎ
Solution :

Q6. If random variable X represents the number of heads when a coin is tossed twice then
mathematical expectation of X is
(a) 0
(b) 1/4
(c) 1/2
(d) 1
Solution :

Q7. The least non-negative remainder when 3
50 is divided by 7 is
(a) 4
(b) 3
(c) 2
(d) 1
Solution :

Q8. If the cash equivalent of a perpetuity of Rs 300 payable at the end of each quarter is 24000
then rate of interest compounded quarterly is
(a) 5%
(b) 4%
(c) 3%
(d) 2%
Solution :

Q9.
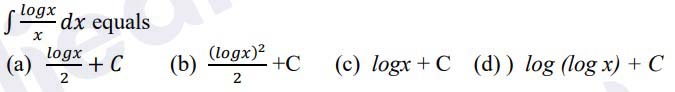
Solution :
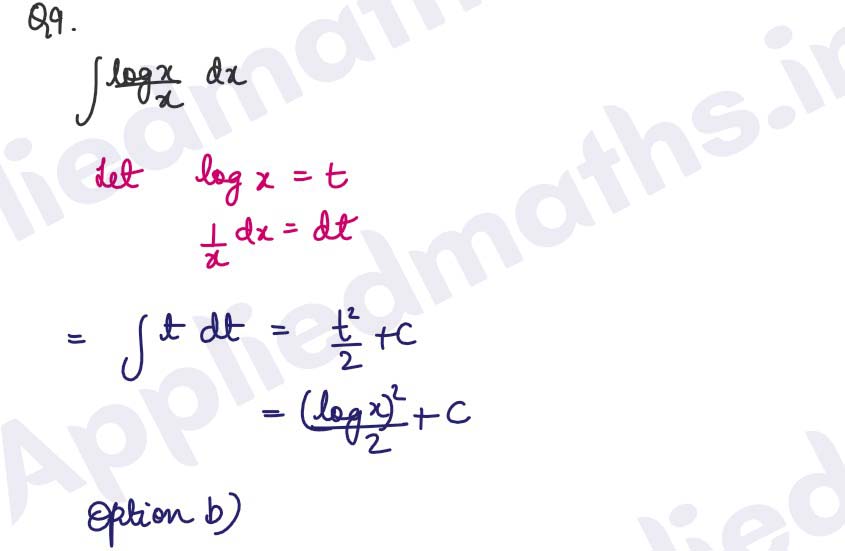
Q10. The supply of finished good was delayed for a month due to landslide in hilly terrain. Under
which trend oscillation does this situation fall
(a) 𝑆𝑒𝑎𝑠𝑜𝑛𝑎𝑙
(b) 𝐶𝑦𝑐𝑙𝑖𝑐𝑎𝑙
(c) 𝑆𝑒𝑐𝑢𝑙𝑎𝑟
(d) 𝐼𝑟𝑟𝑒𝑔𝑢𝑙𝑎r
Solution :

Q11. A machine costing ₹ 30,000 is expected to have a useful life of 4 years and a final scrap value
of ₹ 4000. The annual depreciation is
(a) ₹ 5500
(b) ₹ 6500
(c) ₹ 7500
(d) ₹ 8500
Solution :

Q12. The effective rate of interest equivalent to the nominal rate 6% compounded semi-annually is
(a) 6.05%
(b) 6.07%
(c) 6.09%
(d) 6.1%
Solution :
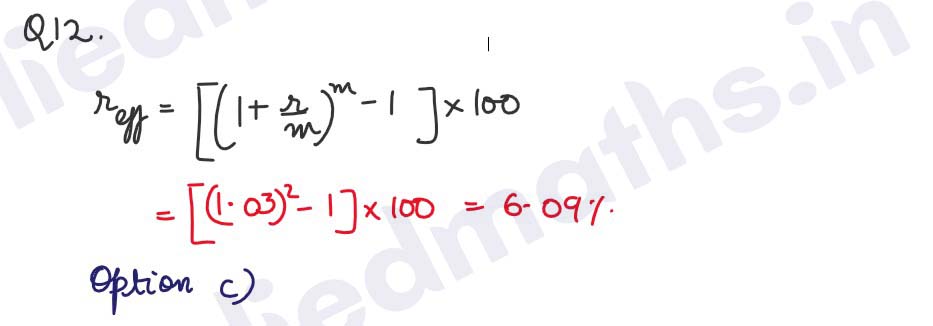
Q13. If the investment of ₹ 20000 in the mutual fund in 2015 increased to ₹ 32000 in year 2020,
then CAGR (Compound Annual Growth rate is) is [Given(1.6)1/5
= 1.098]
(a) 9.08%
(b) 9.8%
(c) 0.098
(d) 0.09
Solution :

Q14.

Solution :

Q15. Besides non negativity constraint the figure given below is subject to which of the following
constraints
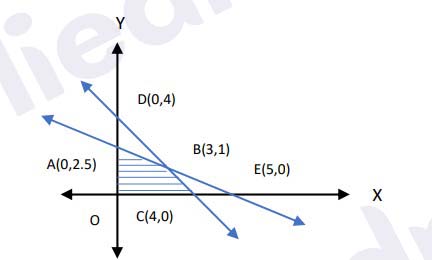
(a) 𝑥 + 2𝑦 ≤ 5 ; 𝑥 + 𝑦 ≤ 4
(b) 𝑥 + 2𝑦 ≥ 5 ; 𝑥 + 𝑦 ≤ 4
(c) 𝑥 + 2𝑦 ≥ 5 ; 𝑥 + 𝑦 ≥ 4
(d) 𝑥 + 2𝑦 ≤ 5 ; 𝑥 + 𝑦 ≥ 4
Solution :

Q16. If X is a Poisson variate such that 3P(X=2) = 2P(X=1) then the mean of the distribution is
equal to
Solution :

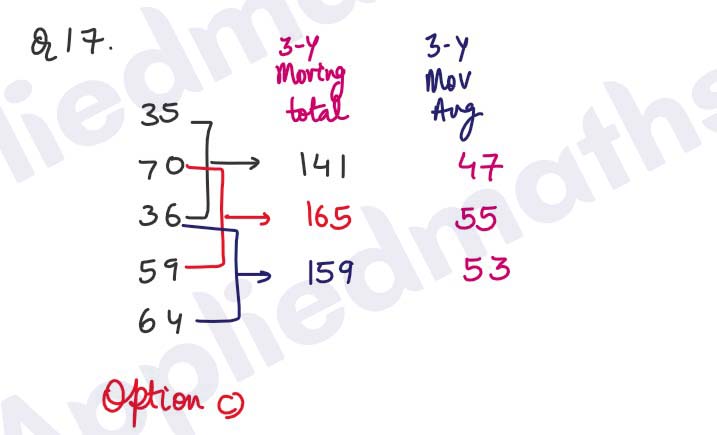
Q17. For the given five values 35, 70, 36, 59, 64, the three years moving averages are given by
(𝑎)47, 53, 55
(b) 53, 47, 45
(c) 47, 55, 53
(d) 45, 55, 57
Solution :
Q18. The data point of a normal variate with mean 12, standard deviation 4 and Z – score 5 is
(a) 28
(b) 304
(c) 34
(d) 32
Solution :

For questions 19 and 20, two statements are given – one labelled Assertion(A) and the other labelled
Reason (R). Select the correct answer to these questions from the codes (i), (ii), (iii) and (iv) as given
below:
(i) Both A and R are true and R is the correct explanation of the assertion
(ii) Both A and R are true but R is not the correct explanation of the assertion
(iii) A is true, but R is false
(iv) A is false, but R is true
(i) Both A and R are true and R is the correct explanation of the assertion
(ii) Both A and R are true but R is not the correct explanation of the assertion
(iii) A is true, but R is false
(iv) A is false, but R is true
Q19. Assertion (A): The maximum profit that a company makes if profit function is given by
P(x) = 41 + 24x-8x2
; where ‘x’ is the number of units and P is the profit is Rs 59
Reason (R) : The profit is maximum at x = a if 𝑃'(𝑎) = 0 𝑎𝑛𝑑 𝑃''(𝑎) > 0
Solution :

Q20.

Solution :
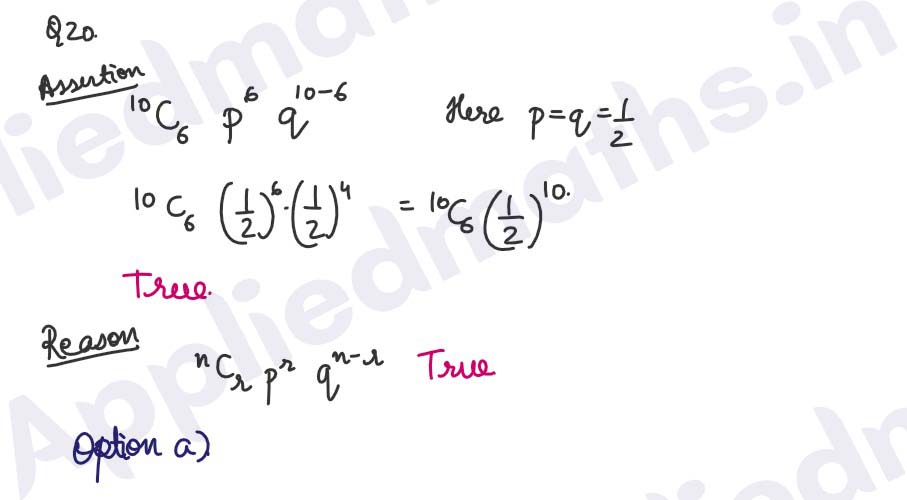
SECTION – B
Q21. At what rate of interest will the present value of perpetuity of 1500 payable at the end of every 6 months be 20,000?
Solution :

Q22.
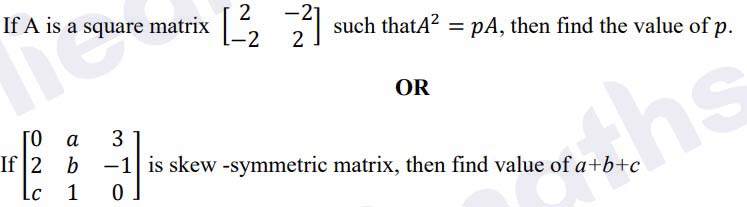
Solution :


Q23. A Cooperative Society of farmers has 10 hectares of land to grow two crops A and B. To control weeds, pesticide has to be used for crops A and B at the rate of 30 grams per hectare and 15 grams per hectare respectively. Further, not more than 750 grams of pesticide should be used. The profit from crops A and B per hectare are estimated as Rs 8000 and Rs 9500. Formulate the above problem as LPP, in order to allocate land to each crop for maximum total profit.
Solution :

Q24. A man rows 15km upstream and 25km downstream each in 5 hours. Find he speed of the stream.
OR
‘A’ can run 40 meters while ‘B’ runs 50 meters in the same time. In a 1000 m race, find by how
much distance ‘B’ beats ‘A’
Solution :

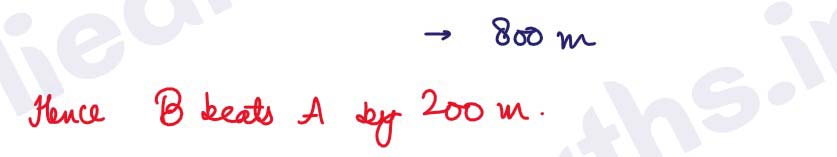
Q25. A machine produces washers of thickness 0.50mm. To determine whether the machine is in proper working order, a sample of 10 washers is chosen for which the mean thickness is 0.53mm and the standard deviation is 0.03mm. Test the hypothesis at 5% level of significance that the machine is working in proper order. [Given 𝑡9(0.05) = 2.262]
Solution :

SECTION-C
Q26.

Solution :


Q27. Cost of two toys A and B are Rs 50 and Rs 75. On a particular Sunday shopkeeper P sells 7 toys of type A and 10 toys of type B whereas shopkeeper Q sells 8 toys of type A and 6 toys of type B. Find income of both shopkeepers using matrix Algebra
Solution :

Q28. Find the intervals in which the function f(x) = 2𝑥 3 − 9𝑥 2 + 12𝑥 − 5 is increasing or decreasing
Solution :

Q29. The demand and supply functions under the pure market competition are 𝑝d = 16 − 𝑥
2
and
𝑝s = 2𝑥2 + 4 respectively, where p is the price and x is the quantity of the commodity. Using
integrals find Consumer’s surplus.
OR
The demand and supply functions under the pure market competition are 𝑝d = 56 − 𝑥2
and
𝑝s = 8 + (x3
/3)
respectively, where p is the price and x is the quantity of the commodity. Using
integrals find Producer’s surplus.
Solution :


Q30. Mr Surya borrowed a sum of Rs 5,00,000 with total interest to be paid Rs 2,00,000(flat) and he is paying an EMI of Rs 12,500. Calculate loan tenure.
Solution :

Q31. Mr Sharma wants to send his daughter abroad for higher studies after 10 years. He sets up a
sinking fund in order to have Rs 500,000 after 10 years. How much should he set aside semiannually into an account paying 5% per annum compounded annually
[Use (1.025)20 = 1.6386]
Solution :

SECTION-D
Q32.On doing the proof reading of a book on an average 4 errors in 10 pages were detected. Using
Poisson’s distribution find the probability of (i) No error and (ii) one error in 1000 pages of first
printed edition of the book
[Use e-0.4 = 0.6703]
OR
How many times Sunil toss a fair coin so that the probability of getting at least one head is
more than 90 %
Solution :


Q33. A manufacturer has three machines I,II and III installed in his factory. Machines I and II are
capable of being operated for at most 12 hours whereas machine III must be operated for at
least 5 hours a day. He produces only two items M and N , each requiring the use of all the three
machines. The number of hours required for producing 1 unit of M and N on three machines
are given in the following table:

He makes a profit of Rs 600 and Rs 400 on one unit of items M and N respectively. Formulate the
above problem as LPP and solve it graphically to find how many units of each item be produced
to maximize profit. Also find the maximum profit.
Solution :


Q34. A company produces a certain commodity with 2400 fixed cost. The variable cost is estimated
to be 25% of the total revenue received on selling the product at a rate of 8 per unit. Find the
following
(i) Cost Function.
(ii) Revenue Function
(iii) Breakeven Point
(iv) Profit Function
OR
The production manager of a company plans to include 180 sq cm of actual printed matter in
each page of a book under production. Each page should have a 2.5 cm wide margin along the
top and bottom and 2 cm wide margin along the sides. What are the most economical
dimensions of each printed page?
Solution :



Q35. The management committee of a Welfare Club decided to award some of its members (say x) for sincerity, some (say y) for helping others selflessly and some others (say z) for effective management. The sum of all the awardees is 12. Three times the sum of all awardees for helping others selflessly and effective management added to two times the number of awardees for sincerity is 33. If the sum of the number of awardees for sincerity and effective management is twice the number of awardees for helping others, use matrix method to find the number of awardees of each category
Solution :

SECTION-E
CASE STUDY – I
Q36. Pipes and Cisterns (Mark 2+1+1) (Internal choice is in the iii part)
A, B and C are three pipes connected to a tank. A and B
together fill the tank in 6 hours. B and C together fill the
tank in 10 hours. A and C together fill the tank in 7(1/2)
ℎ𝑜𝑢𝑟𝑠.
Based on above information answer the following
questions.
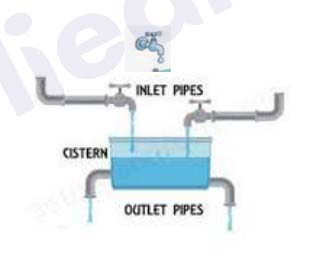
(i) In how much time will A, B and C fill the tank?
(ii) In how much time will A separately fill the tank?
(iii) In how much time will B separately fill the tank?
In how much time will C separately fill the tank?
Solution :
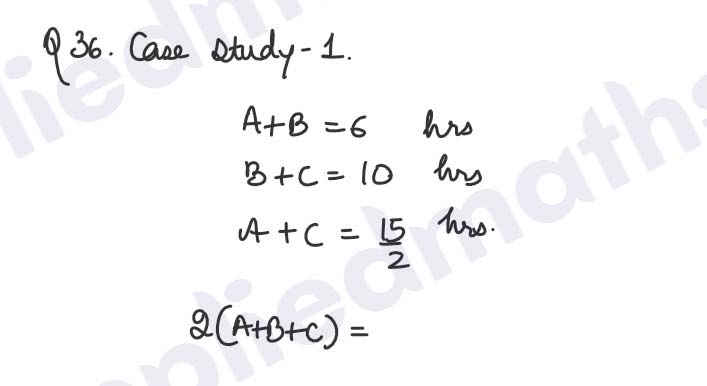
CASE STUDY – II
Q37. Read the following passage and answer the questions given below (Internal
Choice is in option iii.) (Mark 1 + 1 + 2)
Let X denote the number of hours a person watches television during a randomly selected
day. The probability that X can take the values xi, has the following form, where ‘k’ is some
unknown constant
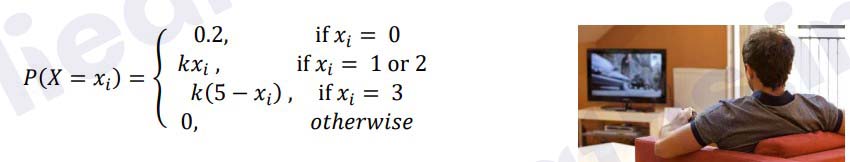
(i) Find the value of k.
(ii) What is the probability that a person watches two hours of television on a selected day?
(iii) What is the probability that the person watches at least two hours of television on a
selected day ?
OR
(iv) What is the probability that the person watches at most two hours of television on a
selected day ?
Solution :


CASE STUDY – III
Q38. When observed over a long period of time, a time series data can predict trend that can forecast
increase or decrease or stagnation of a variable under consideration. Such analytical studies can
benefit a business for forecasting or prediction of future estimated sales or production
The table below shows the welfare expenses(in lakh Rs) of Steel Industry during 2001-2005. Fit a
straight line trend by the method of least squares and estimate the trend for the year 2008.

OR
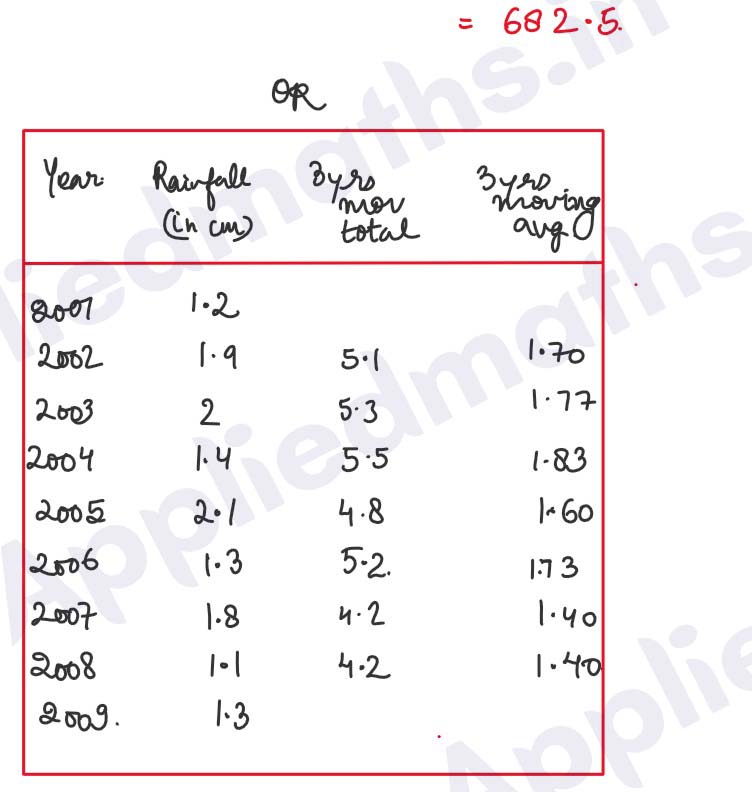
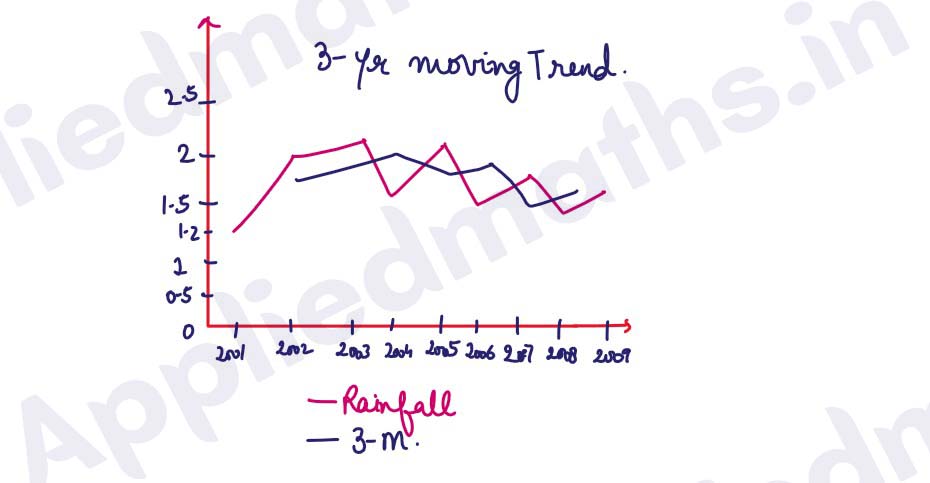
The annual rainfall(in mm) was recorded in Cherrapunji, Meghalaya

Determine the trend of rainfall by three years moving average and draw the moving averages graph.
Solution :