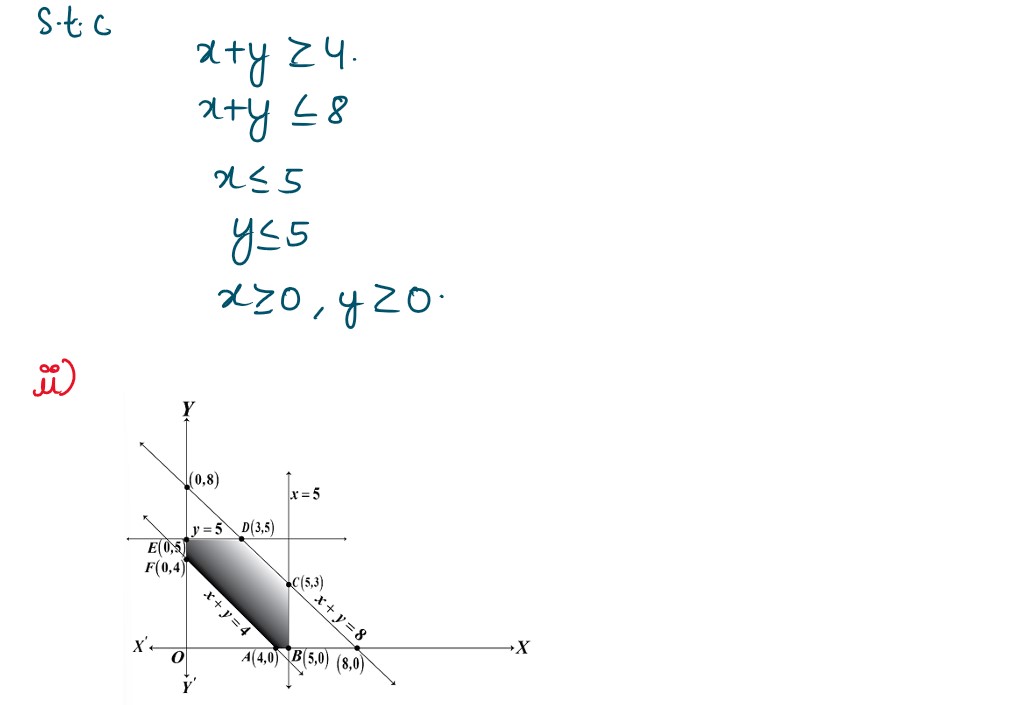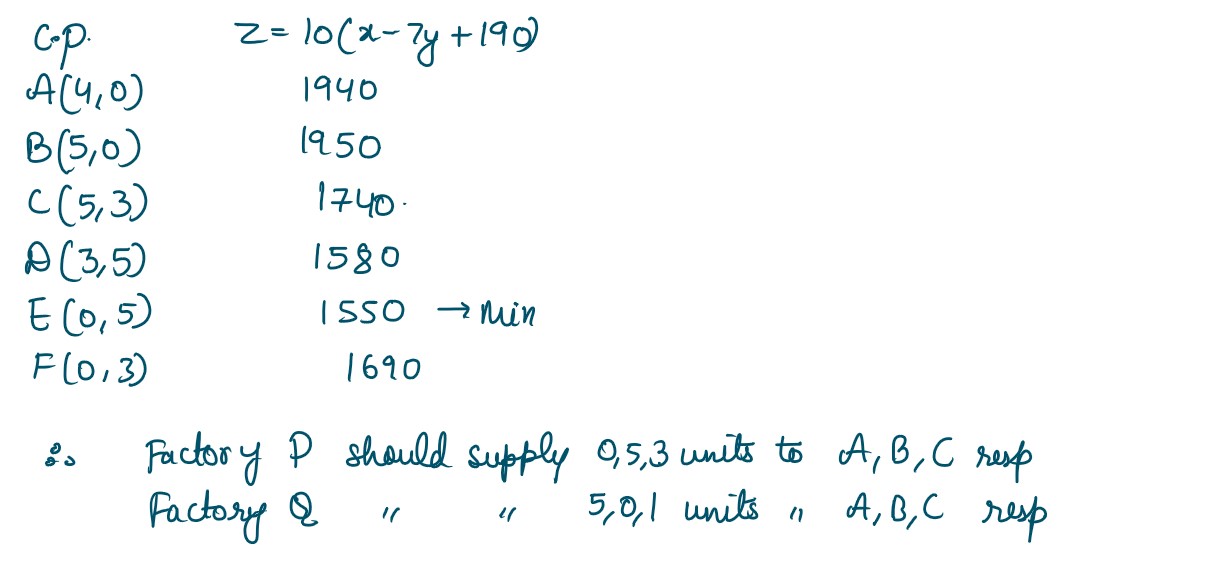Class 12 CBSE Specimen Paper 2025
Class 12 CBSE Applied Maths aims to develop an understanding of basic
mathematical and statistical tools and their
applications in the field of commerce (business/ finance/economics) and social
sciences. Topics covered in Class 12th Applied Maths includes : Numbers, Quantification and
Numerical Applications, Algebra, Calculus, Probability Distributions , Inferential Statistics, Index
Numbers and Time-based data , Financial Mathematics , Linear Programming.
SECTION β A
Q1. The area (in sq units) bounded by the curve π¦ = βπ₯, the
x β axis, π₯ = 1 and π₯ = 4 is
(A) ππ/π
(B) π/π
(C) ππ/π
(D) ππ/3
Solution :
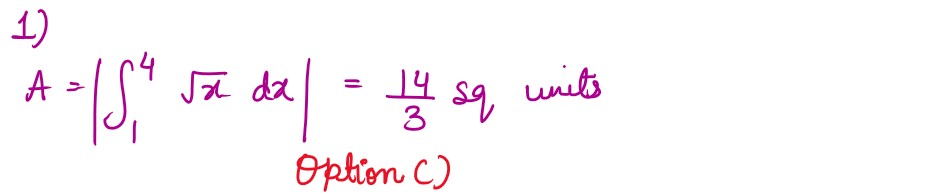
Q2. Sampling which provides for a known non-zero equal chance of selection is
(A) Systematic sampling
(B) Convenience sampling
(C)Quota sampling
(D) Purposive sampling
Solution :
Q3. Let the cost function for a manufacturer is given by
C(x) = x3/3 -x2 + 2x
(In rupees)
Which of the following statement is correct based on the above information?
(A)The marginal cost decreases from 0 to 1 and then increases onwards.
(B) The marginal cost increases from 0 to 1 and then decreases onwards.
(C) Marginal cost decreases as production level increases from zero.
(D)Marginal cost increases as production level increases from zero.
Solution :
Q4. The absolute minimum value of the function f(x) = 4x - (1/2)x2 in the interval [-2,9/2] is
(A) β8 (B) β9 (C) β10 (D) β16
Solution :
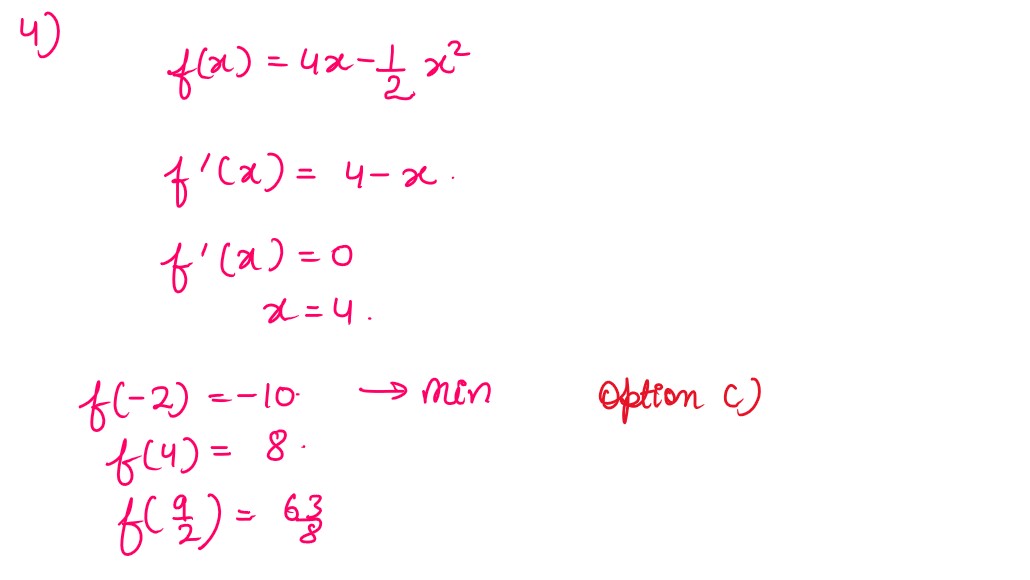
Q5. For the purpose of
t β test of significance, a random sample of size
(n) 2025
is drawn from a
normal population, then the degree of freedom (π) is
(A)
20252025
(B)
20252024
(C)
2025
(D)
2024>
Solution :
Q6. The constraints of a linear programming problem along with their graphs is shown below:
x+2y ≥ 3, x≥10,y≥0
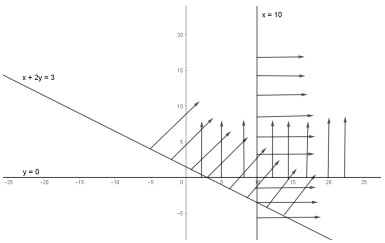
Which of the following inequality may be removed so that the feasible region remains the
same in above graph?
(A) π₯ + 2π¦ β₯ 3
(B) π₯ β₯ 10
(C) π¦ β₯ 0
(D) π₯ β₯ 0
Solution :
Q7. A player rolls one fair die. If the die shows an odd number, the player wins the value that
appears on the die, else loses half the value that appears on it. The expected gain of the player
is
(A) β
π/
π
(B) π
(C)
π/
π
(D) 1
Solution :
Q8. The original cost of a machine is βΉ
1200000
and the scarp value of the machine after a useful
life of 3 years is βΉ
300000
, then the book value of the machine at the end 2 years is
(A) βΉ
100000
(B) βΉ
250000
(C) βΉ
600000
(D) βΉ
800000
Solution :
Q9. A fish jumps out of the water surface and follows the parabolic path
y = 6x - x2 - 8; 2 ≤ x ≤ 4.
The fish reaches the highest height in its path at
( 3,1) . The slope of the path of the fish at
( 3,1)
is
(A) 0
(B) 1
(C) 2
(D) 3
Solution :
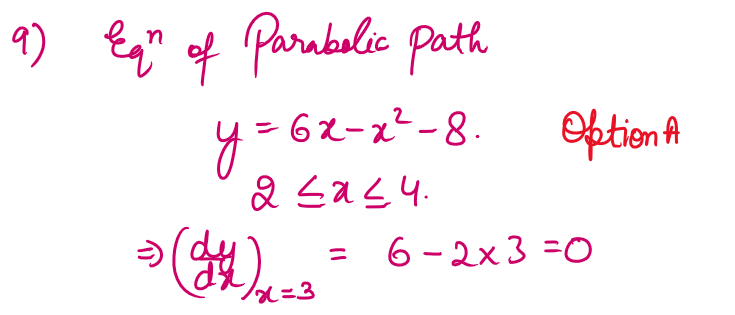
Q10. In a large consignment of electric bulbs
5%
of a batch of batteries are defective. A random
sample of 80 is taken for inspection with replacement. Then the Variance of the number of
defectives in the sample, is
(A)
18/5
(B)
19/5
(C)
4.555
(D) 8
Solution :
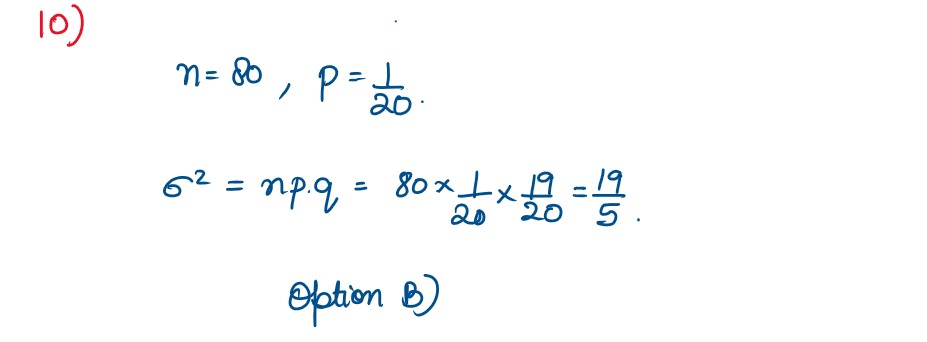
Q11. If it is currently 6: 00 pm in 12 hours clock then what will be the time after 375 hours?
(A) 6 am (B) 6 pm (C) 9 am (D) 9 pm
Solution :
Q12. The values of 1/π₯
for the given values of π₯ β (β1,3) β {0} is
(A) (β1,1/3) βͺ (3, β)
(B) (ββ, β1) βͺ (1/3, β)
(C) (β1/3, 1)
(D) (β1/3, β1)
Solution :
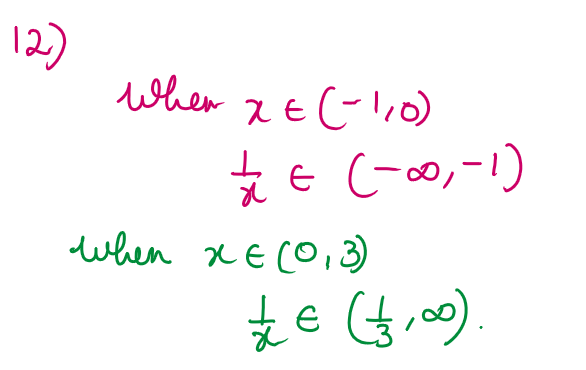
Q13. The component of a time series attached to long term variations is termed as
(A) Seasonal variations
(B) Irregular variations
(C) Secular trend variations
(D) Cyclic variations
Solution :
Q14.
The present value of a sequence of payments of βΉ 800 made at the end of every 6 month
and continuing forever. If money is worth
4%
per annum compounded semi-annually, then the
present value of the sequence is:
(A) βΉ 20000
(B) βΉ 40000
(C) βΉ 60000
(D) βΉ 80000
Solution :
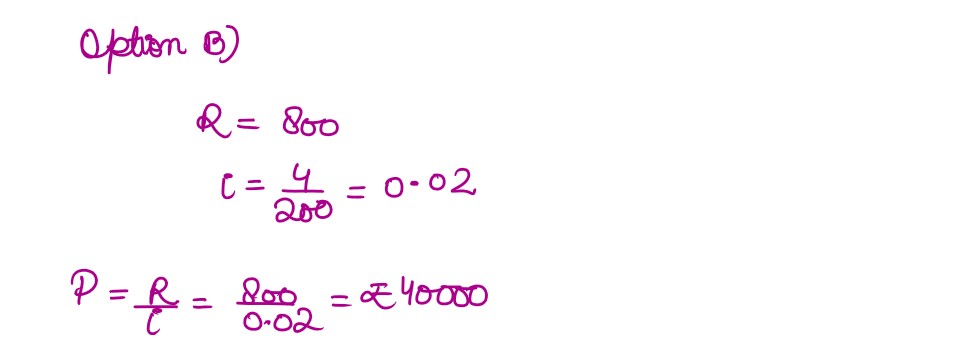
Q15. Shown below is a curve.
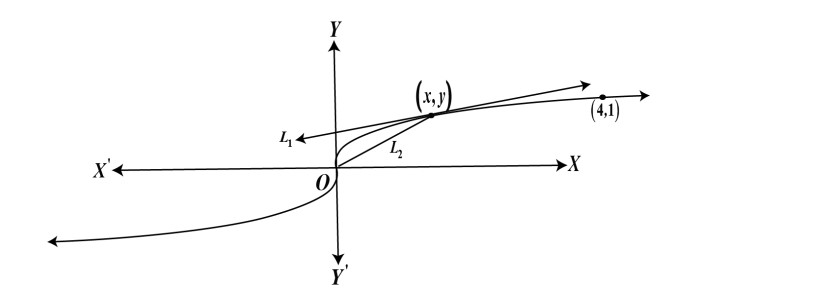
L1
is the tangent to any point
( x y, )
on the curve.
L2
is the line that connects the point
( x y, )
to the origin.
The slope of
L1
is one third of the slope of
L2
.
Then the differential equation, using the given conditions is:
Solution :
Q16. For a 3 Γ 3 matrix if adj A = 2Aβ1, find |3AAT|
(A) 108 (B) 12 (C) 54 (D) 8
Solution :
Q17. For two matrices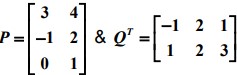 
( where QT is the transpose of the matrix Q) , P-Q
Solution :
Q18. The order and degree of a differential equation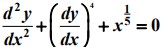 
; respectively, are
(A) 2 and 4
(B) 2 and 1
(C) 2 and 3
(D) 3 and 3
Solution :
For questions 19 and 20, two statements are given β one labelled Assertion(A) and the other labelled
Reason (R). Select the correct answer to these questions from the codes (i), (ii), (iii) and (iv) as given
below:
(i) Both A and R are true and R is the correct explanation of the assertion
(ii) Both A and R are true but R is not the correct explanation of the assertion
(iii) A is true, but R is false
(iv) A is false, but R is true
(i) Both A and R are true and R is the correct explanation of the assertion
(ii) Both A and R are true but R is not the correct explanation of the assertion
(iii) A is true, but R is false
(iv) A is false, but R is true
Q19. Assertion (A): The effective rate of interest equivalent to a nominal rate of
6%
when
compounded continuously is equal to
e0 06 - 1 = 1.618% .
Reason (R): The relation between effective rate
(reff )
of interest and nominal rate
(r)
of
interest: reff
= er - 1
where
'e' - Eulerβs number (approximate value is
2.71828
), when
compounded continuously
Solution :
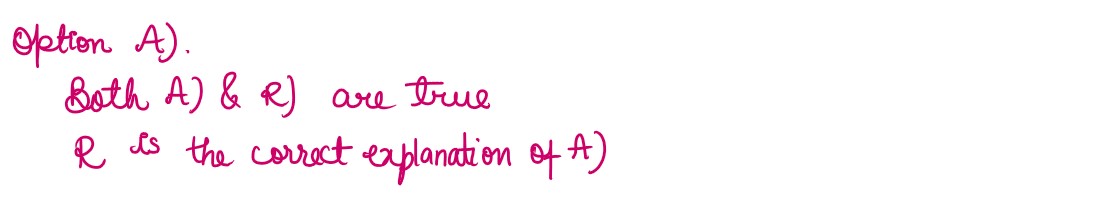
Q20.
Assertion(A): π΄ = [πππ] =
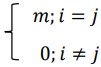
where π is a scalar, is an identity matrix if π = 1
Reason (R): Every identity matrix is not a scalar matrix
Solution :
SECTION β B
Q21. (a) In what ratio water must be added in milk costing βΉ 60 per litre, so that the resulting
mixture would be of worth βΉ 50 per litre?
OR
(b) A pump can fill a tank with water in 2 hours. Because of leakage, it took 7/3 hrs to fill the
tank. How much time will it take for the leakage to drain all the water in the full tank?
Solution :
Q22. In a 200 π race, A can give a start of 18 π to B and a start of 31 π to C. In a race of 350 π, how much start can B give to C?
Solution :
Q23. A boat takes thrice as long to go upstream to a point as to return downstream to the starting point. If the speed of the stream is 5ππ/β, find the speed of the boat in still water.
Solution :
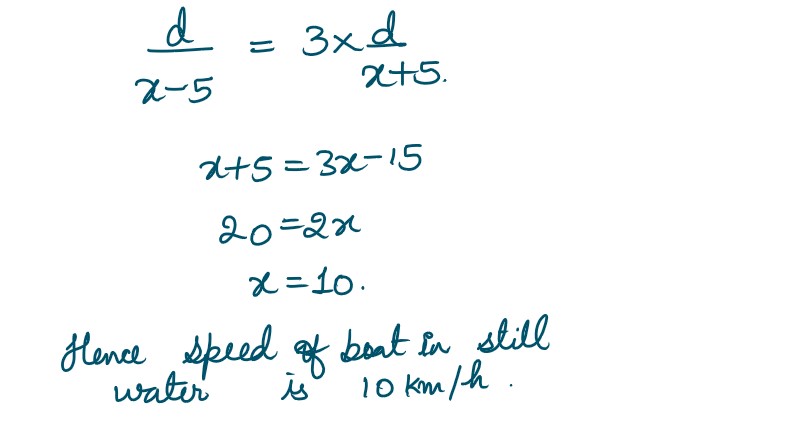
Q24. (a) The incidence of occupational disease in an industry is such that the workers have a 20%
chance of suffering from it. What is the probability that out of six workers 4 or more will catch
the disease?
OR
(b) The lifetime of an item produced by a machine has a normal distribution with mean 12
months and standard deviation of 2 months. Find the probability of an item produced by this
machine will last
(i) less than 7 months
(ii) between 7 and 14 months
(Given P(Z < 5/2) = 0.9938 and P(Z < 1) = 0.8413)
Solution :
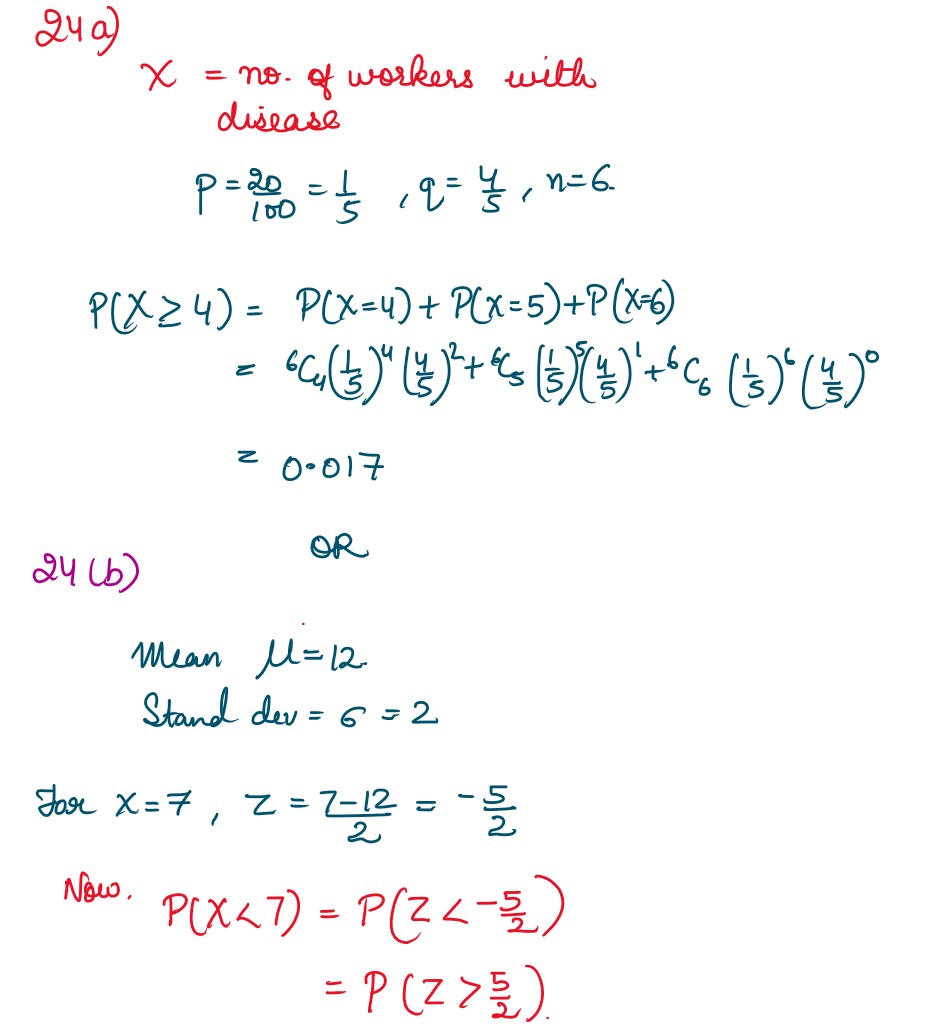
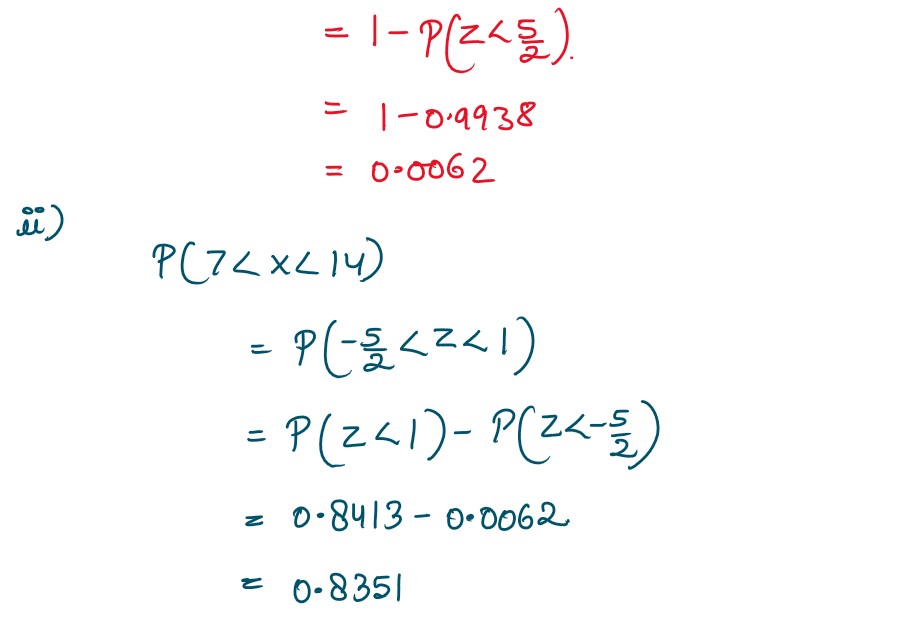
Q25. If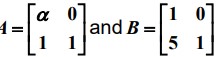 
then find the value of α (if exists) for which A2 = B
Solution :
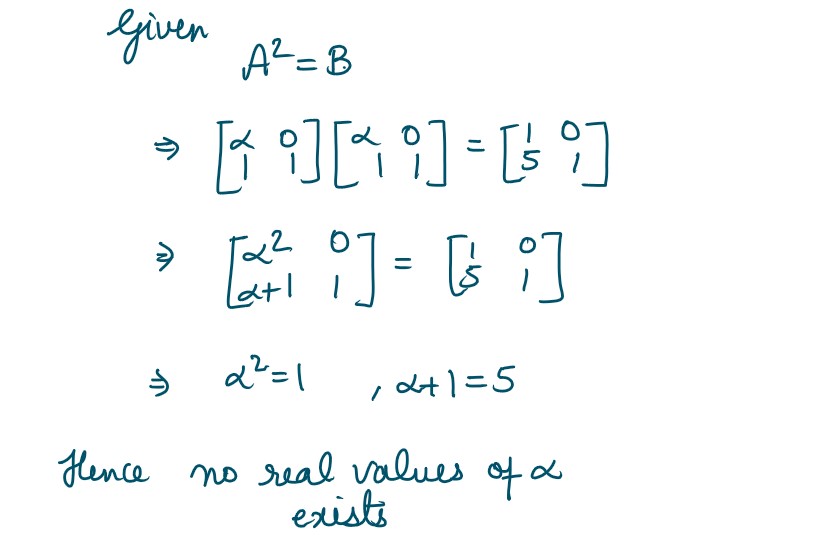
SECTION-C
Q26. Find the remainder when 561 is divided by 7
Solution :
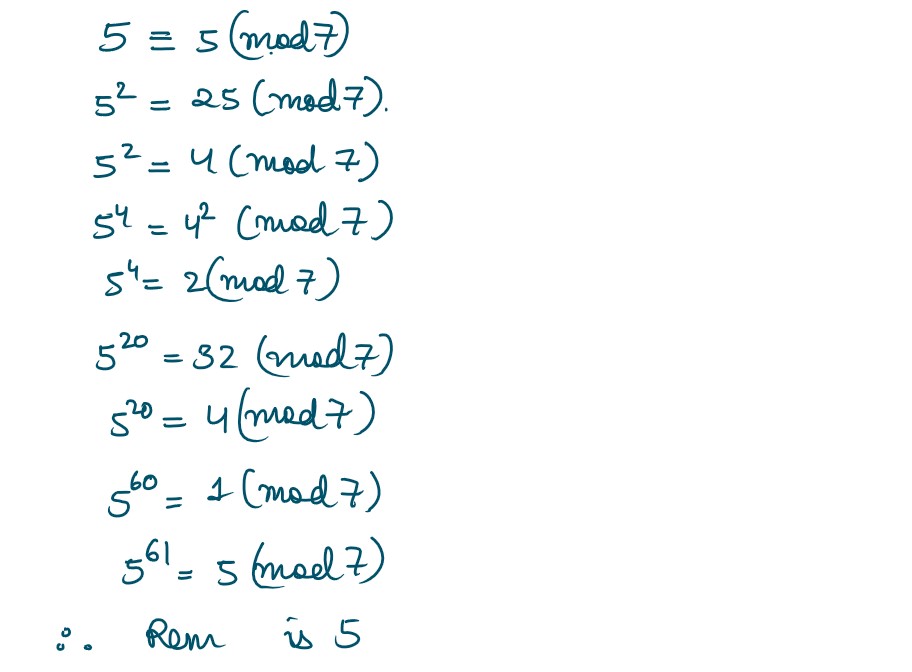
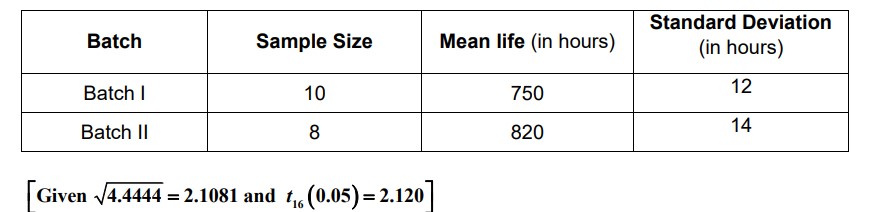
Q27. (a) Two batches of the same product are tested for their mean life. Assuming that, the lives
of the product follow a normal distribution with an unknown variance; test the hypothesis that
the mean life is the same for both the branches, given the following information:
OR
(b) The manufacturer of electrical items makes bulbs and claims that these bulbs have a
mean life of 25 months. The life in months of a random sample of 6 such bulbs are given to be
24, 26, 30, 20, 20 and 18. Test the validity of the manufacturerβs claim at 1% level of significance.
[Given π‘5
(0.01) = 4.032]
Solution :
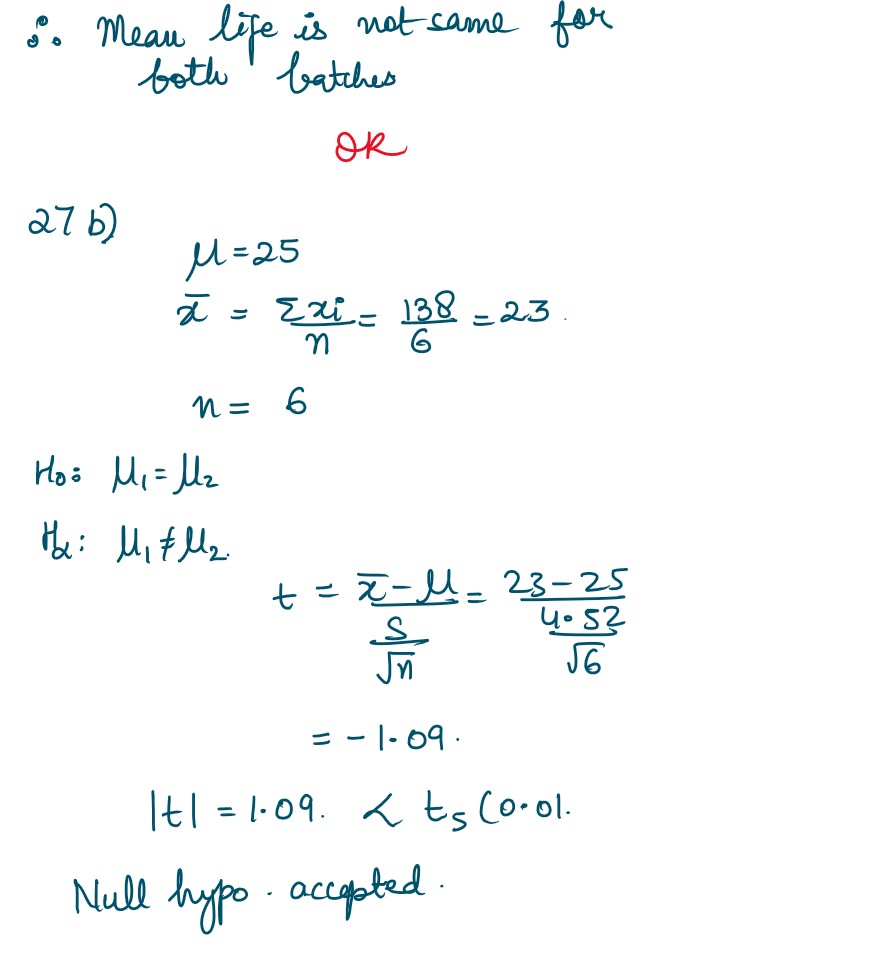
Q28. A traffic engineer records the number of bicycle riders that use a particular cycle track. He records that an average of 3.2 bicycle riders use the cycle track every hour. Given that the number of bicycles that use the cycle track follow a Poisson distribution, what is the probability that 2 or less bicycle riders will use the cycle track within an hour? Also find the mean expectation and variance for the random variable. (Given π β3.2 = 0.041)
Solution :
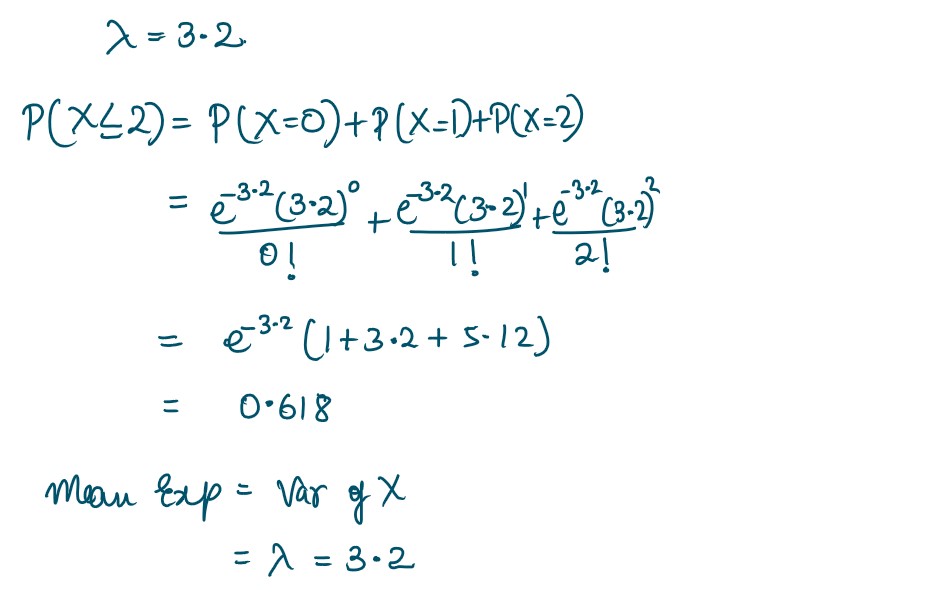
Q29. Mr Rohit invested βΉ 5000 in a fund at the beginning of year 2021 and by the end of year 2021 his investment was worth βΉ 9000. Next year market crashed and he lost βΉ 3000 and ending up with βΉ 6000 at the end of year 2022. Next year i.e. 2023 he gained βΉ 4500 and ending up with βΉ 10500 at the end of the year. Find CAGR (Compounded Annual Growth Rate) of his investment. (Use (2.1)1/3 = 1.2805)
Solution :
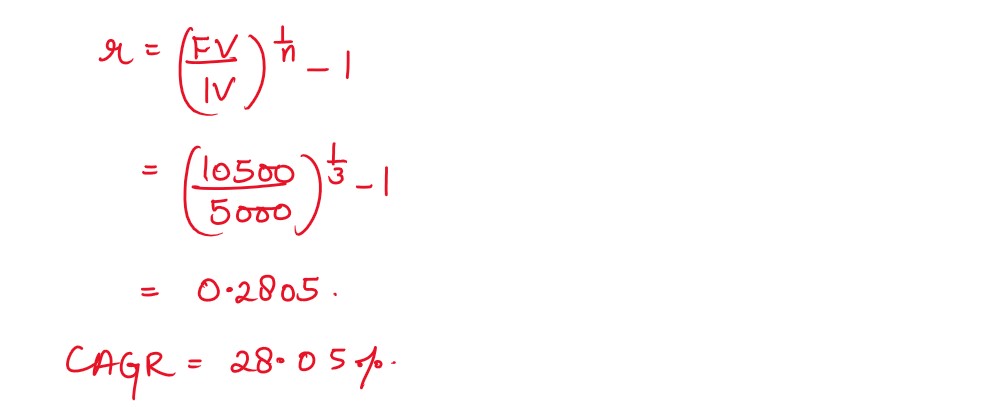
Q30. A small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 25. It takes one hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 14. If the profit on a necklace is βΉ 100 and that on a bracelet is βΉ 300, formulate an L.P.P. for finding how many of each should be produced daily to maximize the profit? It is being given that at least one of each must be produced.
Solution :
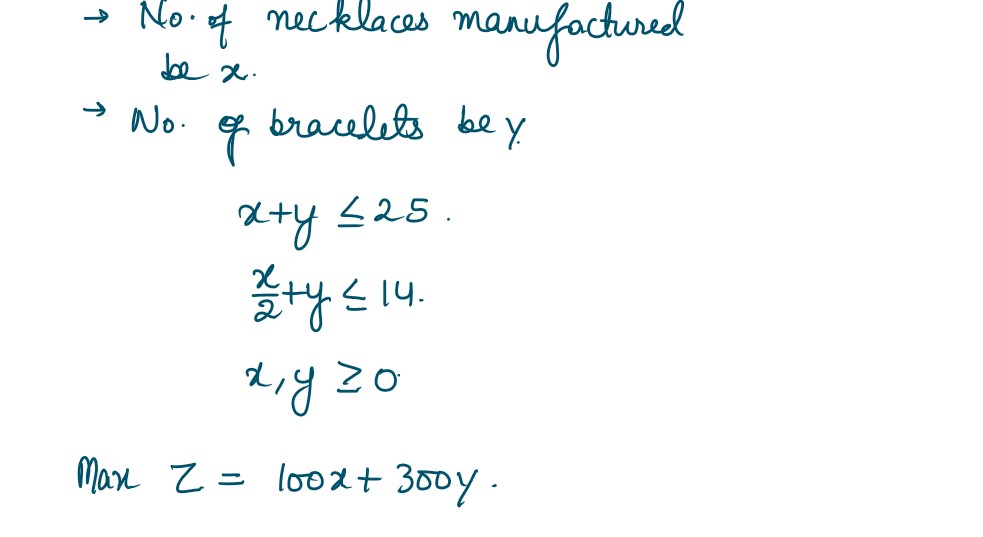
Q31. (a) An octagonal prism is a three-dimensional polyhedron bounded by two octagonal bases
and eight rectangular side faces. It has 24 edges and 16 vertices.
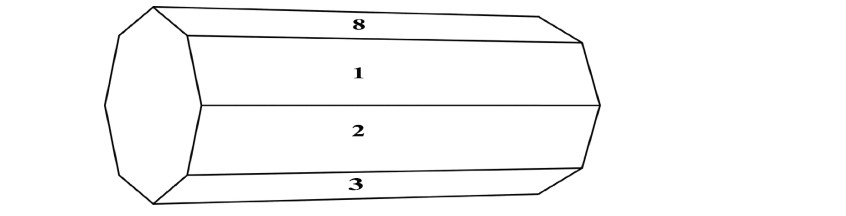
The prism is rolled along the rectangular faces and number on the bottom face (touching the
ground) is noted. Let
X
denotes the number obtained on the bottom face and the following table
gives the probability distribution of
X
On the above context, answer the following questions.
(i) Find the value of
p .
(ii) Find the mean,
E (X)
OR
(b) If the probability of success in a single trial is
0.01 , how many minimum number of Bernoulli
trials must be performed in order that the probability of at least one success is 1/2 or more ? (Use log10 2 = 0.3010 and log10 99 = 1.9956)
Solution :
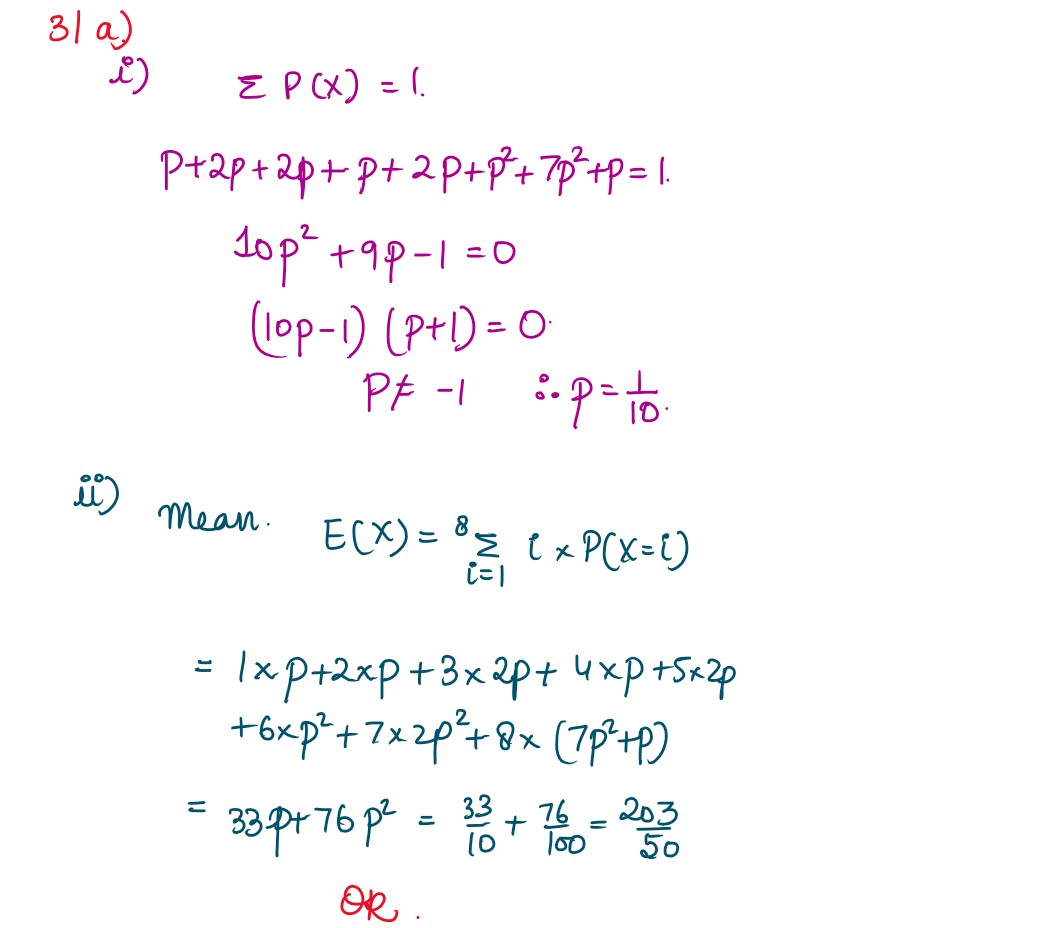
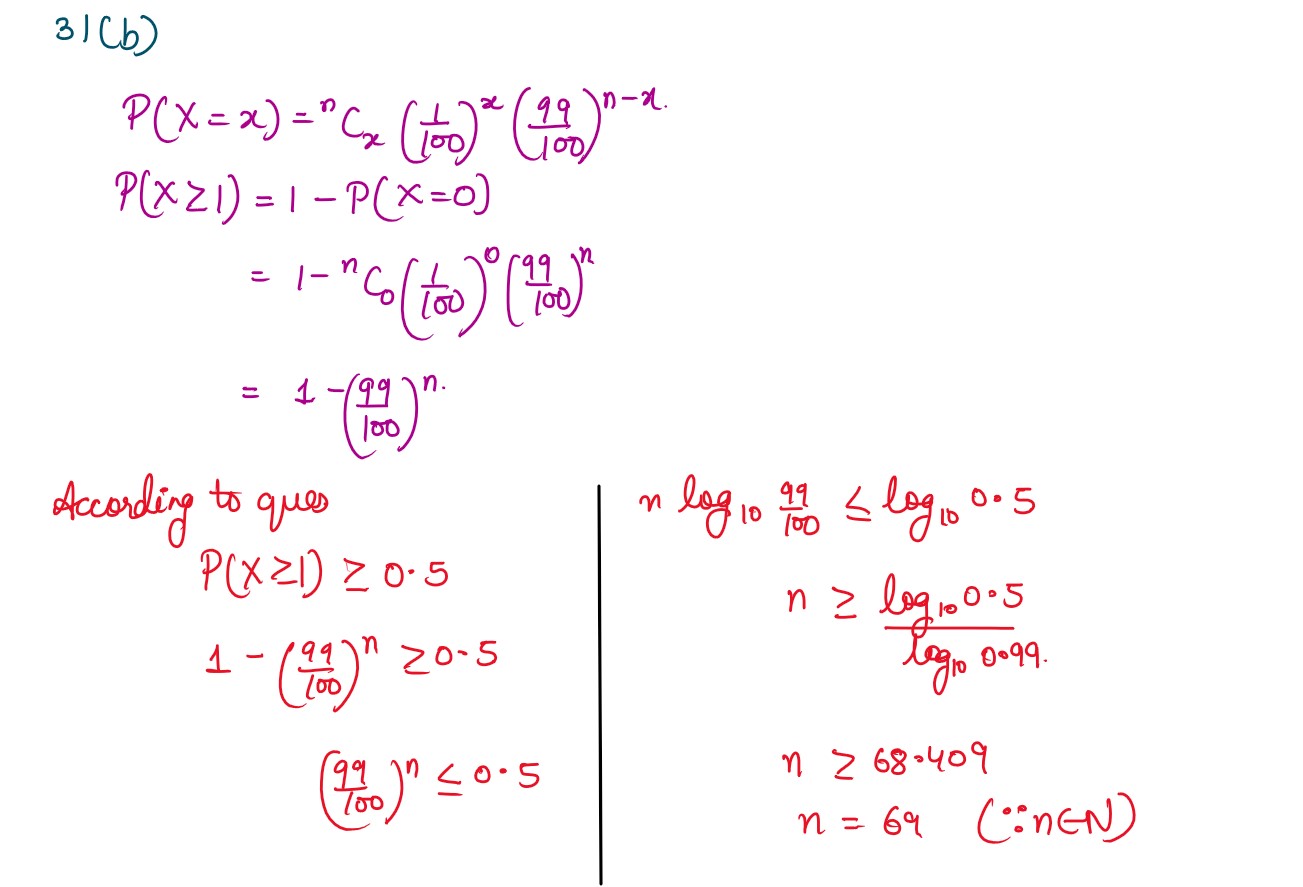
SECTION-D
Q32. (a) Fit a straight-line trend by using the method of least squares for the following data
and calculate the trend values
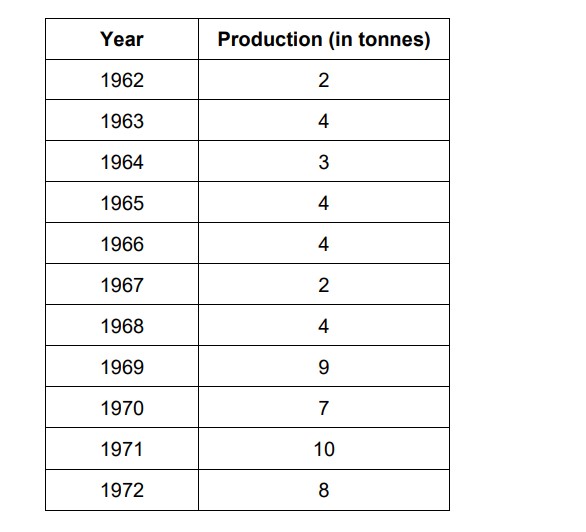
OR
(b) The quarterly profits of a small-scale industry (βΉ in thousands) are as follows.
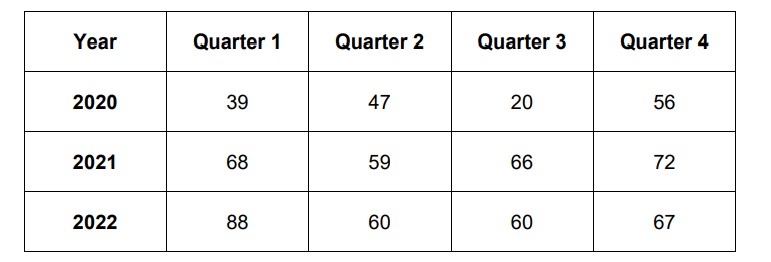
Calculate 4-quarterly moving averages.
Solution :
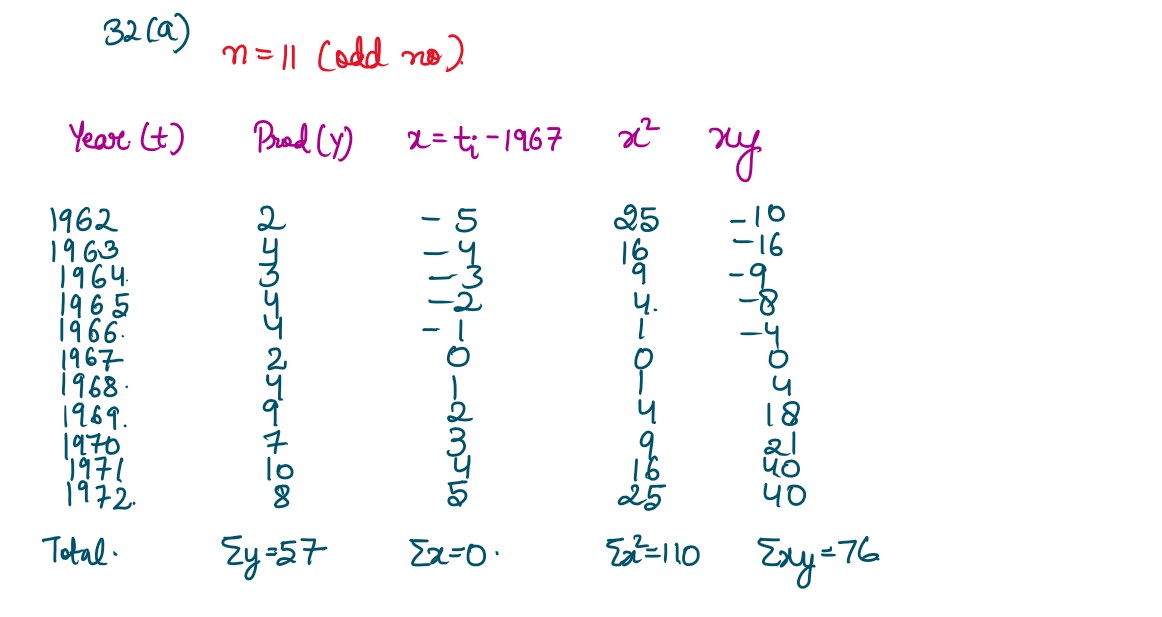
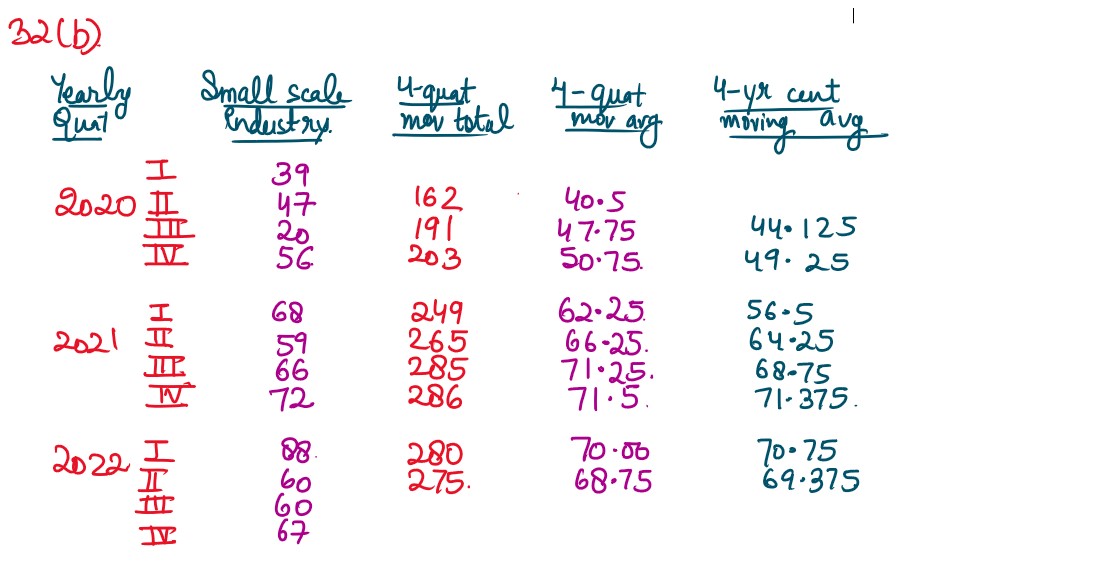
Q33. (a) An owl was sitting at
(0,k) ; k > 0. Then it starts flying along the path whose equation
is given by y = ax2 + bx + c where
a ∈ R - {0} ,b,c ∈ R . It passes through the points (1,2) , (2,1 )
and
(4,5). Using Cramerβs Rule, find the values of π, π, π and hence k.
OR
(b) A toy rocket is fired, from a platform, vertically into the air, its height above the ground
after t seconds is given by s(t) = at2 + bt + c where a,b,c ∈ R; a ≠ 0 and
s(t) is measured in metres. After 10 second, the rocket is 16 m above the ground; after 20 seconds, 22 m; after
30 seconds, 25 m.
(i) Write down a system of three linear equations in terms of
a b,
and
c .
(ii) Hence find the values of
a b,
and
c
, using matrix method
Solution :
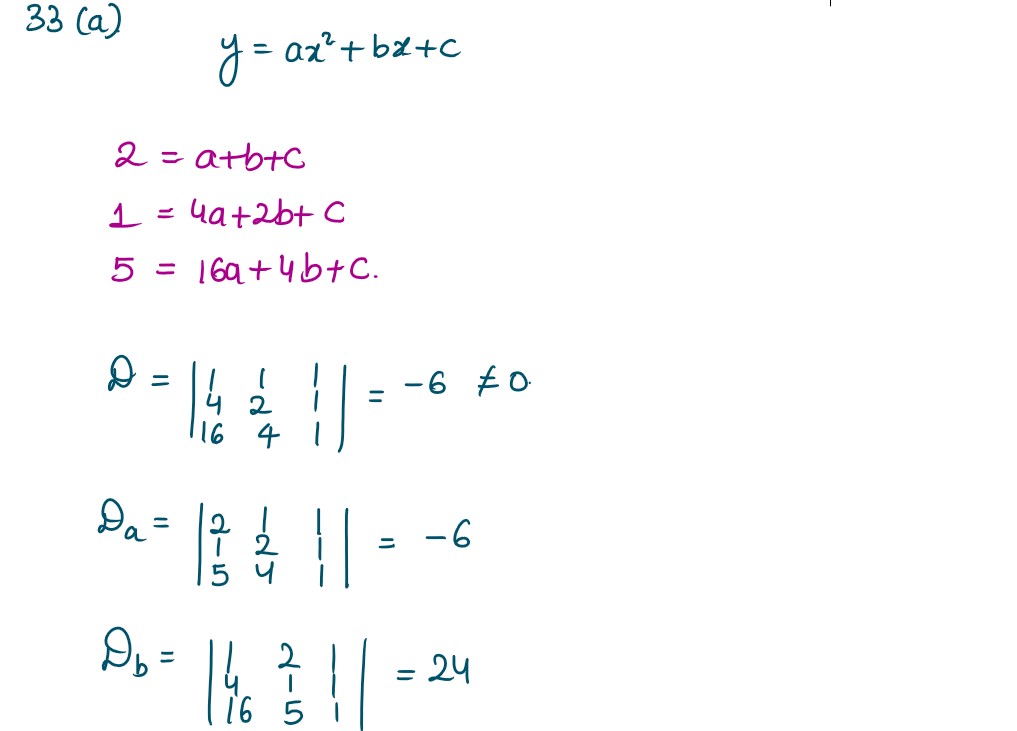
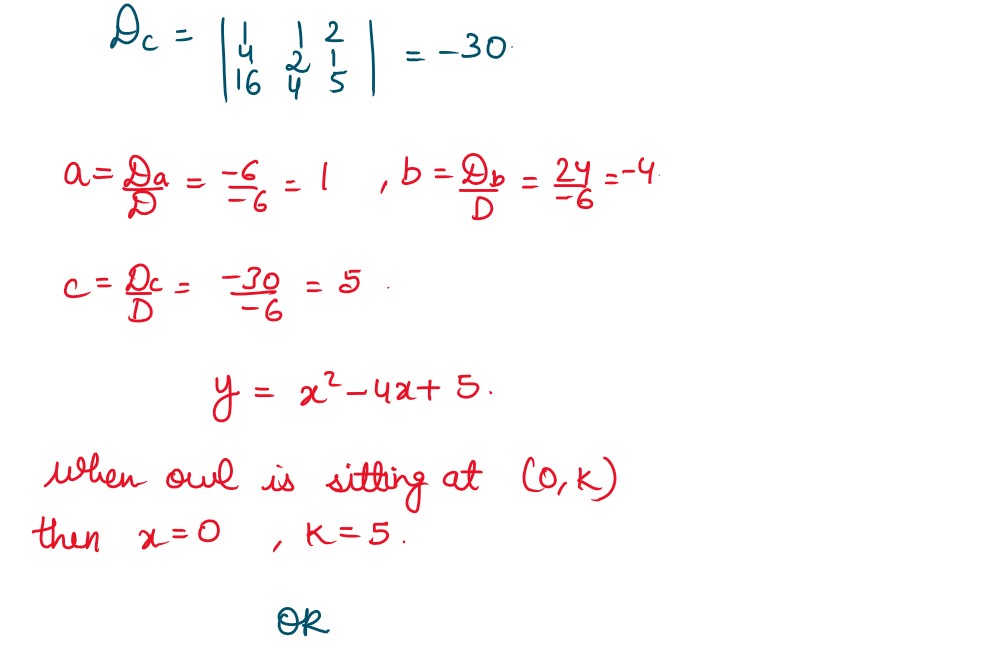
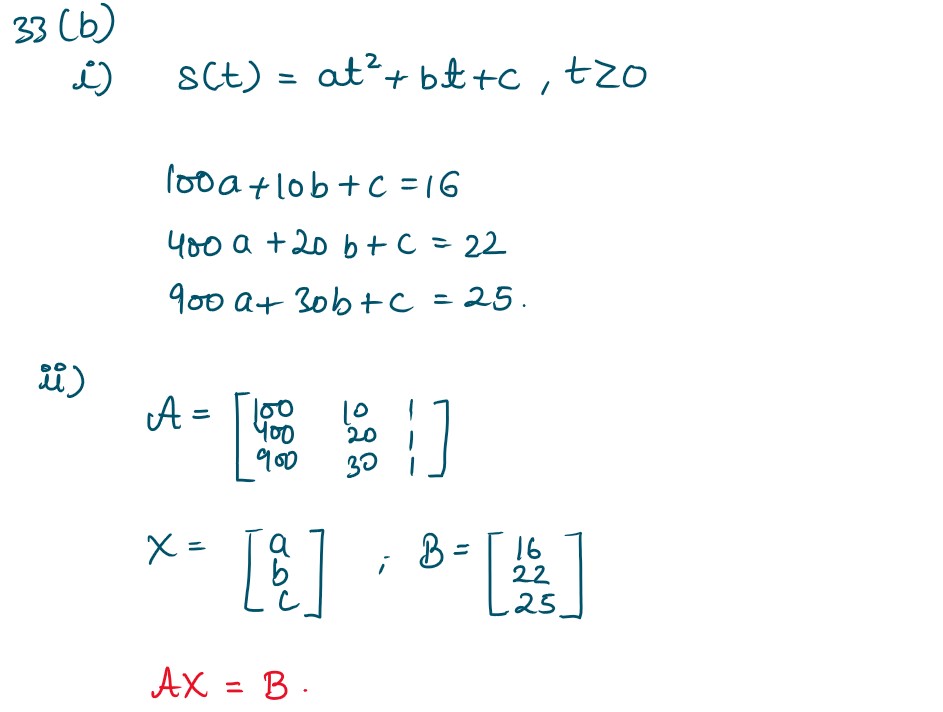
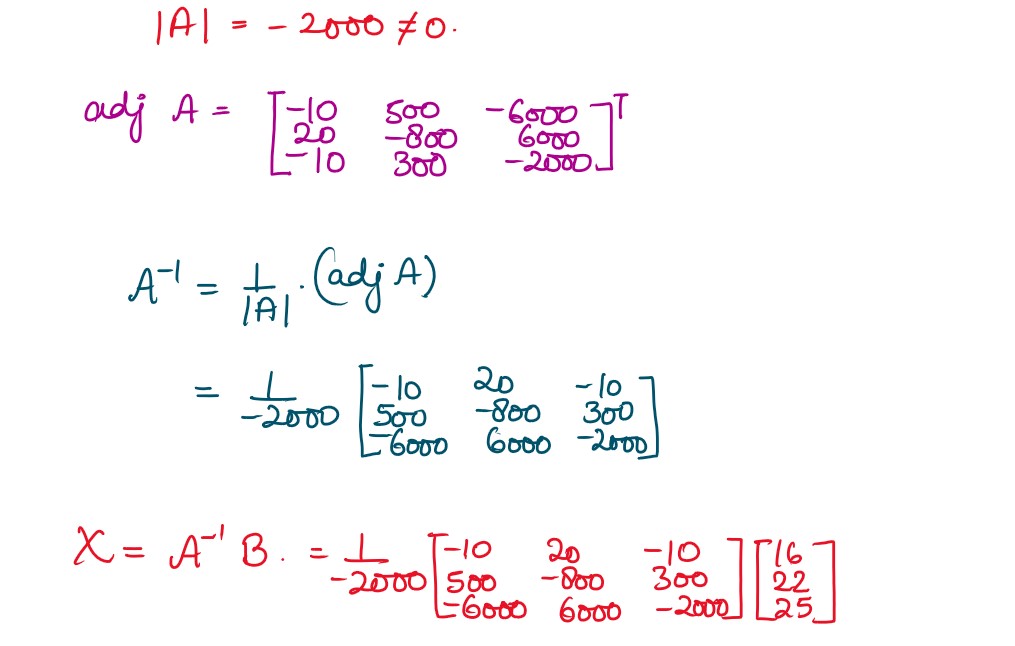
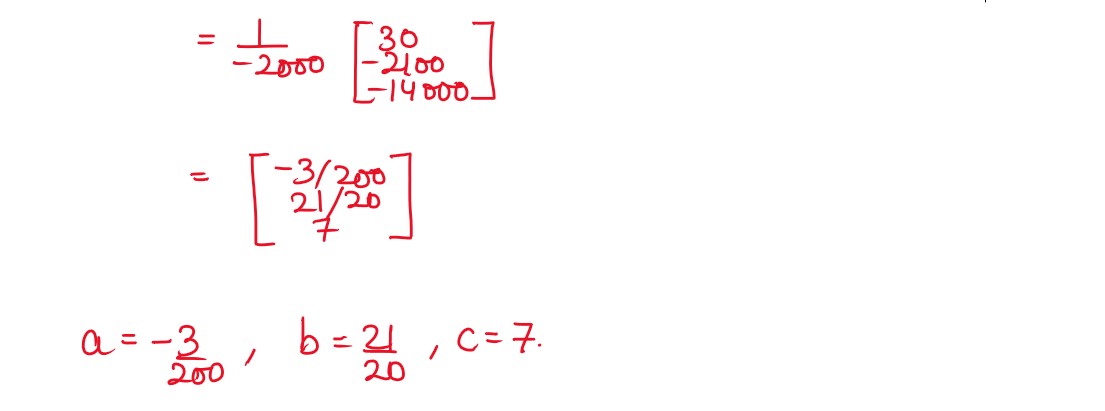
Q34. Supply and demand curves of a tyre manufacturer company is given below:
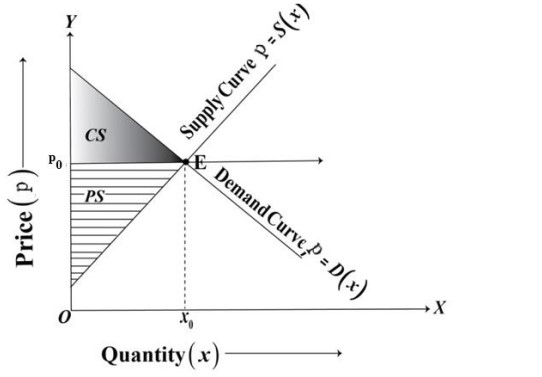
The above graph showing the demand and supply curves of a tyre manufacturer company which
are linear. 'ABC' tyre manufacturer sold 25 units every month when the price of a tyre was βΉ 20000
per units and 'ABC' tyre manufacturer sold 125 units every month when the price dropped to βΉ
15000 per unit. When the price was βΉ 25000 per unit, 180 tyres were available per month for sale
and when the price was only βΉ 15000 per unit, 80 tyres remained. Find the demand function. Also
find the consumer surplus if the supply function is given to be πΊ(π) = πππ π + 7000
Solution :
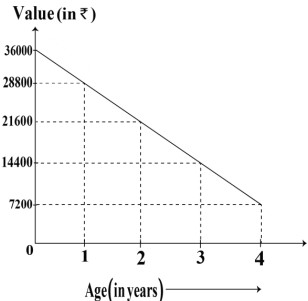
Q35. In 4 years, a mobile costing βΉ 36,000 will have a salvage value of βΉ 7200.
The following graph shows the depreciation of a mobileβs value over 4 years
A new mobile at that time (i.e., after 4 years) is expected to cost for βΉ 55,200. In order to
provide funds for the difference between the replacement cost and the salvage cost, a sinking
fund is set up into which equal payments are placed at the end of each year. If the fund earns
interest at the rate
7%
compounded annually, how much should each payment be? Also find
the amount of Annual Depreciation of the mobileβs value over 4 years and find the rate of
depreciation (under straight line method). Use (1.07)4 = 1.3107
Solution :
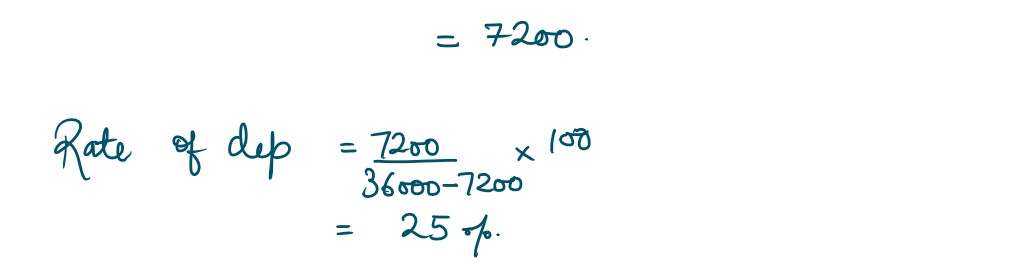
SECTION-E
CASE STUDY β I
Q36. A student Shivam is running on a playground along the curve given by
y = x2 + 7.
Another student Manita standing at point
(3, 7)
on playground wants to hit Shivam by paper ball when
Shivam is nearest to Manita.
Based on above information, answer the following questions:
(i) Let at any instant while running along the curve
y = x2 + 7 , Shivamβs position be
(x,y). Find the expression for the distance (D) between Shivam and Manita in terms of 'x' .
(ii) Find the critical point(s) of the distance function.
(iii) (a) What is the distance between Shivam and Manita when they are at least distance
from each other.
OR
(iii) (b) Find the position of Shivam, when he is closest to Manita
Solution :
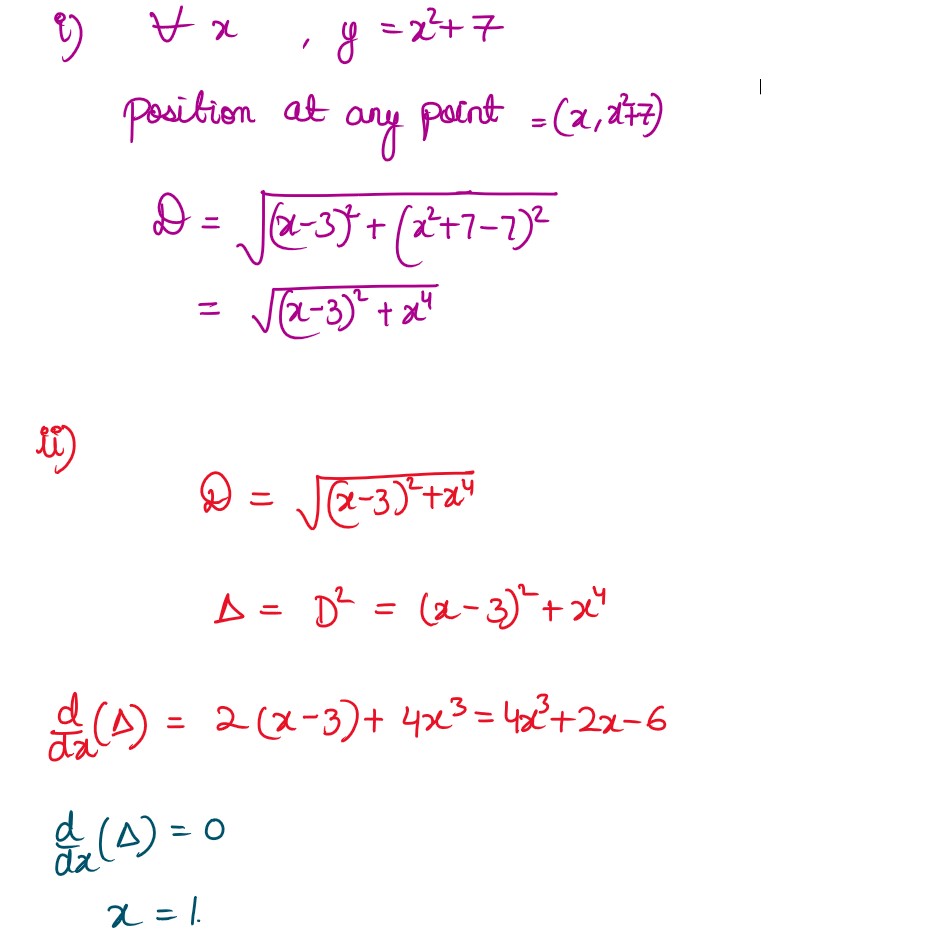
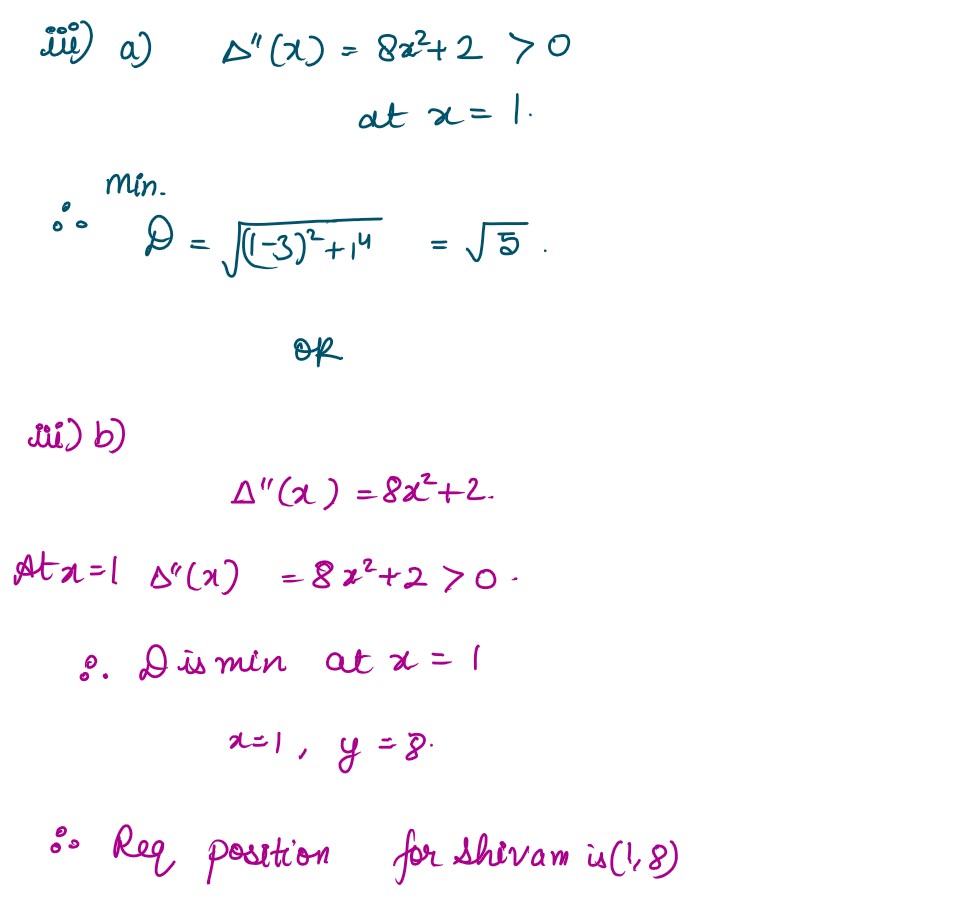
CASE STUDY β II
Q37. EQUATED MONTHLY INSTALMENTS (EMI): -
Each instalment can be considered as consisting of two parts:
(i) Interest on the outstanding loan
(ii) Repayment of part of the loan.
Methods of calculation of EMI or Instalment: -
EMI or Installment can be calculated by two methods:
1.
Flat Rate Method
2.
Reducing-balance method or Amortization of Loan
Rajesh purchased a house from a company for βΉ
2500000
and made a down payment of βΉ
500000
He repays the balance in
25 years
by monthly instalments at the rate of
9%
per annum
compounded monthly. (Given (1.0075)-300 = 0.1062)
Based on the above information, answer the following questions:
(i) Find the number of payments and find the rate of interest per month.
(ii) (a) What are the monthly payments of instalments using reducing balance method?
OR
(ii) (b) What are the monthly payments of instalments using flat rate method?
(iii) What is the total interest payment made in the process applied to calculate EMI in the
above part
(37(ii))
?
Solution :
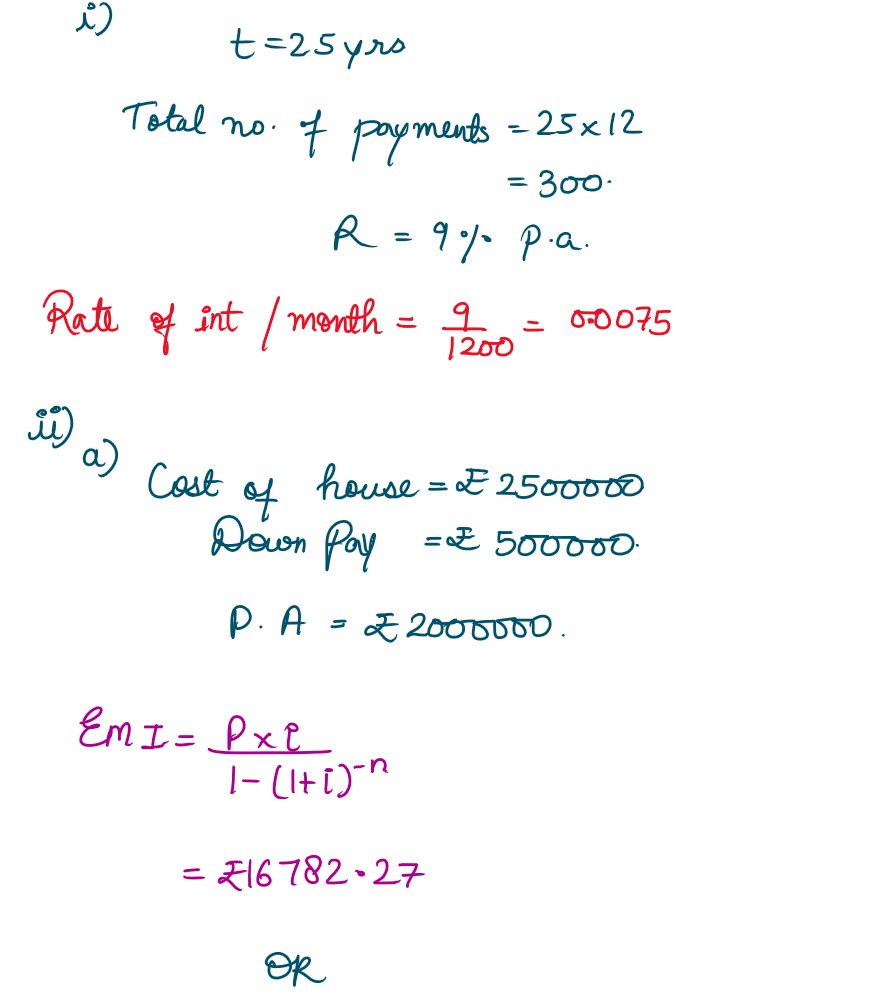
CASE STUDY β III
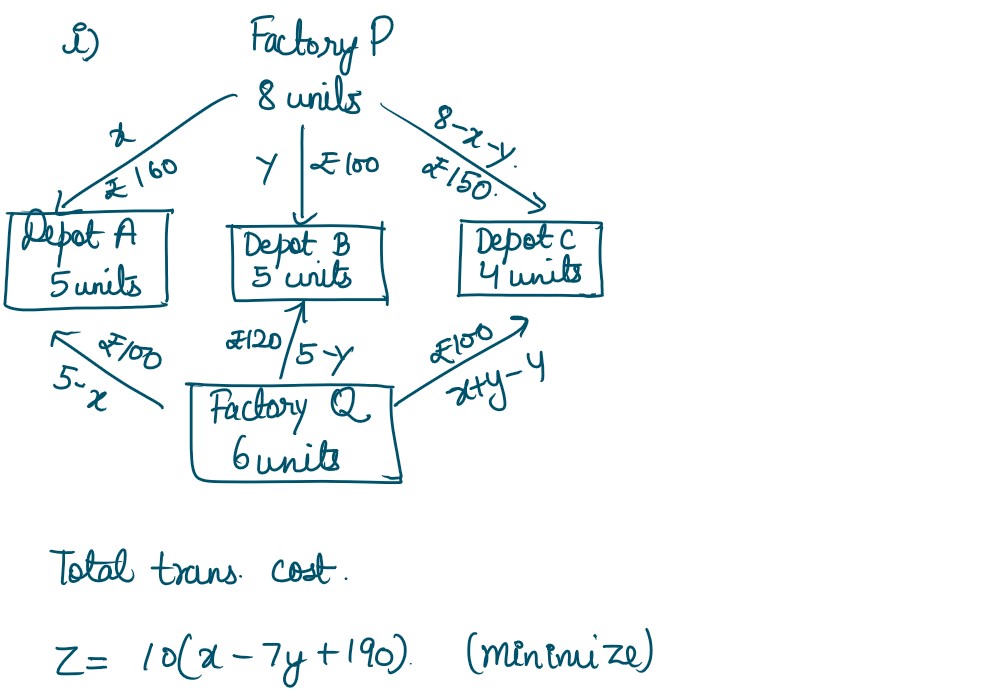
Q38. A company has two factories located at P and Q and has three depots situated at A, B and
C. The weekly requirement of the depots at A, B and C is respectively 5, 5 and 4 units, while
the production capacity of the factories P and. Q are respectively 8 and 6 units. The cost (in
βΉ) of transportation per unit is given below
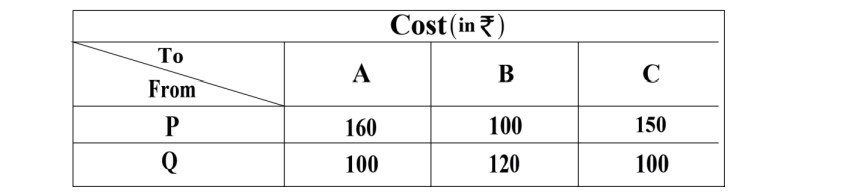
Based on the above information, answer the following questions:
(i) Formulate the objective function and the constraints of the above Linear programming
problem
(ii) How many units should be transported from each factory to each depot in order that
the transportation cost is minimum?
Solution :
