Class 12 CBSE Applied Maths Numerical Inequalities Exercise 2.2
Class 12 CBSE Applied Maths aims to develop an understanding of basic
mathematical and statistical tools and their
applications in the field of commerce (business/ finance/economics) and social
sciences. Topics covered in Class 12th Applied Maths includes : Numbers, Quantification and
Numerical Applications, Algebra, Calculus, Probability Distributions , Inferential Statistics, Index
Numbers and Time-based data , Financial Mathematics , Linear Programming.
Please Select
Q1.
Solve 7x-1< 5x+3 when
(i) x is an integer
(ii)x is a real number
Solution :

See the following (2 to 5) inequalities for real x:
Q2.
(i) 4x-3≤6x+7
(ii) 3x -7 > 5x-1
Solution :

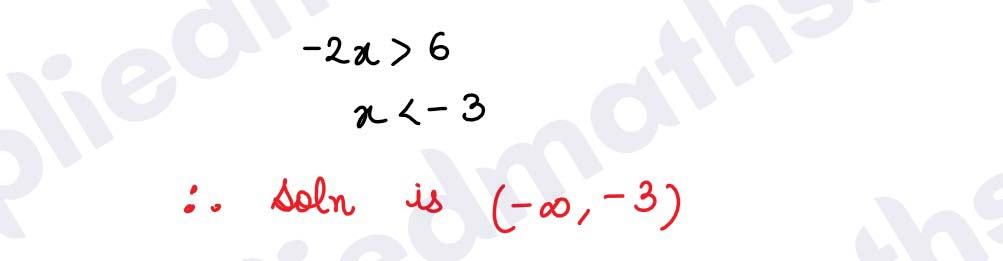
Q3.
(i) 2(2x+3)-10≤6(x-2)
(ii) 37-(3x+5)≥9x-8(x-3)
Solution :


Q4.
(i) x+x/2 + x/3 < 11
(ii) x/3 > x/2 +1
Solution :


Q5.
(i) 2x-3/4 + 8 ≥2+ 4x/3
(ii) 5-2x/3 ≤ x/6 -5
Solution :


Q6. The marks obtained by Sukriti in first two unit tests are 75 and 70. Find the number of minimum marks she should get in the third unit test to have an average of atleast 60 marks.
Solution :
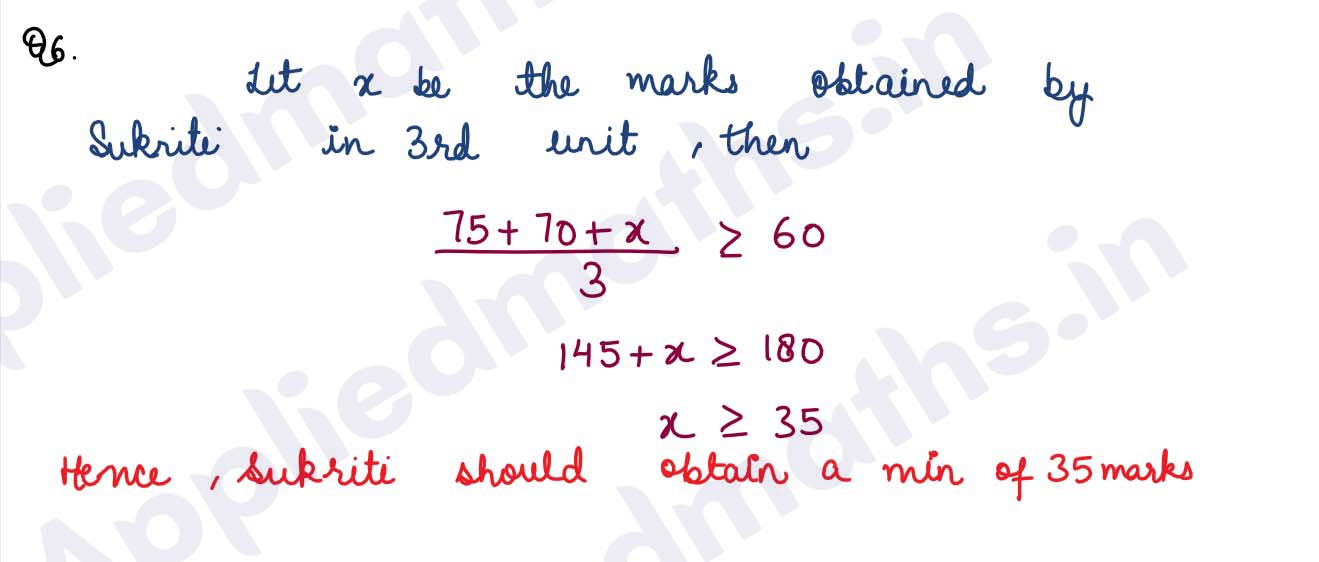
Q7.
Satyarth and Swarit are brothers, Satyarth owns a house which is worth ₹3 crores and Swarit was a
farmhouse which is worth ₹2.75 crores. But Satyarth has a debt of ₹55 lakhs. If they both sell their
properties, then which of the following statement(s) holds true to represent
the above data mathematically:
(a) Satyarth's net worth is more than Swarit's net worth.
(b) Swarit's net worth is more than Satyarth's net worth,
(c) 2.45 < 2.75
Solution :

Q8.
If a, b, c are positive real numbers, then prove that the following using A.M.-G.M. inequality.
(i) (1+a2)(1+b2) ≥ 4ab
(ii) (a2b + b2c + c2a)(ab2+bc2+
ca2) ≥ 9a2b2c2
(iii) (a+b)2 ≥ 4ab
Solution :

Q9. If x is a positive mal number, then find the smallest value of x2+361/x
Solution :
