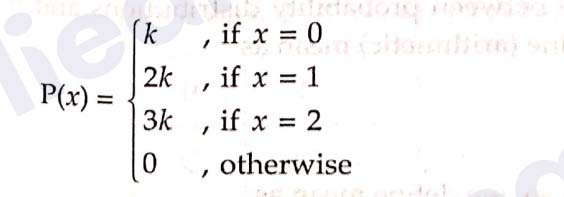Class 12 CBSE Applied Maths Probability Exercise 9.1

Class 12 CBSE Applied Maths aims to develop an understanding of basic mathematical and statistical tools and their applications in the field of commerce (business/ finance/economics) and social sciences. Topics covered in Class 12th Applied Maths includes : Numbers, Quantification and Numerical Applications, Algebra, Calculus, Probability Distributions , Inferential Statistics, Index Numbers and Time-based data , Financial Mathematics , Linear Programming.


Please Select

Exercise 9.2 Exercise 9.3 Exercise 9.4 Exercise 9.5 Exercise 9.6

Q1. A random variable X has the probability distribution:



(i) Determine the value of a.
(ii) Find P(X< 3),p(x≥4),P(0< X< 5)

View Solution  



Q2. A random variable X has the probability distribution:



If events E={X is a prime number} and F={X< 4},then find P(E ∪ F).

View Solution  



Q3. A random variable X has the probability distribution where k is some number:



(i) Determine the value of k.
(ii) Find P(X< 2),p(X ≤ 2),P(X ≥ 2)

View Solution  



Q4. A coin is tossed twice (or two coins are tossed simultaneously).

(i) Find the probability distribution of X, the number of heads.

(ii) Ifa random variable Y is defined on this sample space as the number of tails, then find the probability distribution of Y.

View Solution  



Q5. A die is rolled. If a random variable X is defined as the number on the upper face, then find its probability distribution.

View Solution  



Q6. An urn contains 5 white and 3 black balls. If two balls are drawn at random without replacement and X denotes the number of white balls drawn, then find its probability distribution.

View Solution  



Q7. Two cards are drawn simultaneously from a well-shuffled pack of 52 cards. Find the probability distribution of the number of jacks.

View Solution  



Q8. Four bad oranges are mixed accidentally with 16 good oranges. Find the probability distribution of the number of bad oranges in a draw of two oranges.

View Solution  



Q9. Three balls are drawn one by one without replacement from a bag containing 5 white and 4 red balls. Find the probability distribution of the number of white balls drawn.

View Solution  



Q10. A box contains 12 bulbs of which 3 are defective. A sample of 3 bulbs is selected from the box. Let X denote the number of defective bulbs in the sample. Find the probability distribution of X.

View Solution  



Q11. Four bad eggs are mixed with 10 good ones. If 3 eggs are drawn one by one without replacement, then find the probability distribution of the number of bad eggs drawn.

View Solution  



Contact Us