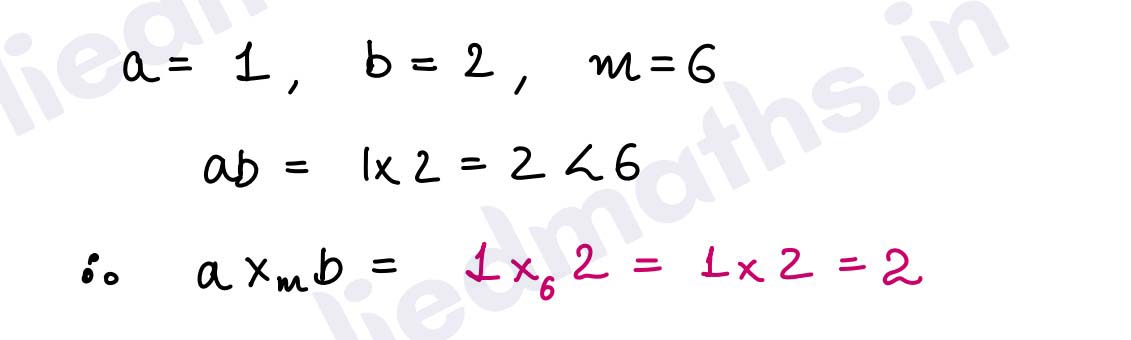Numbers, Quantification & Numerical Application Chapter Important Questions
Class 12 CBSE Applied Maths aims to develop an understanding of basic mathematical and statistical tools and their
applications in the field of commerce (business/ finance/economics) and social
sciences. Topics covered in Class 12th Applied Maths includes : Numbers, Quantification and
Numerical Applications, Algebra, Calculus, Probability Distributions , Inferential Statistics, Index Numbers and Time-based data , Financial Mathematics , Linear Programming.
Please Select
It is a system of arithmetic for integers where numbers " wrap around " when reaching a certain value called the modulus (mod).

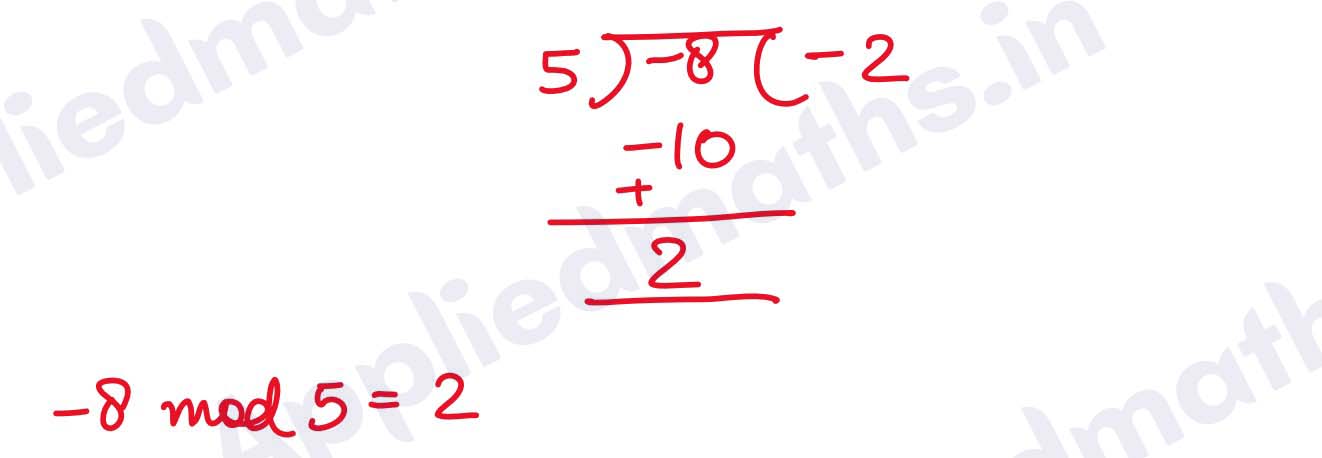
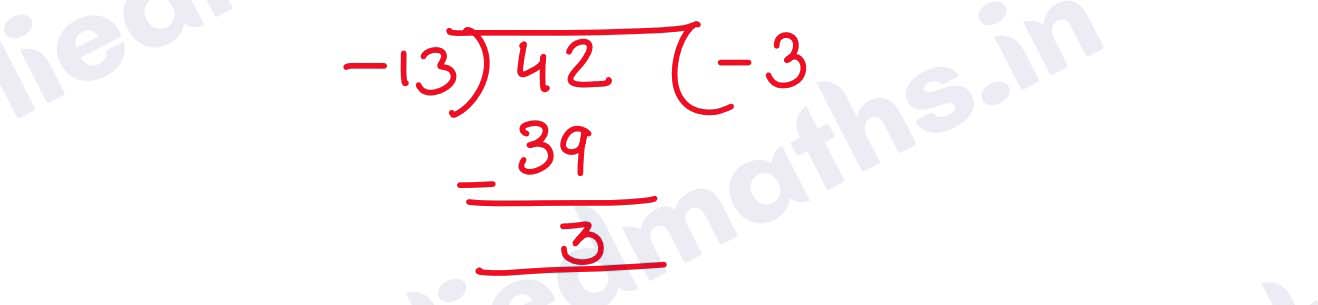
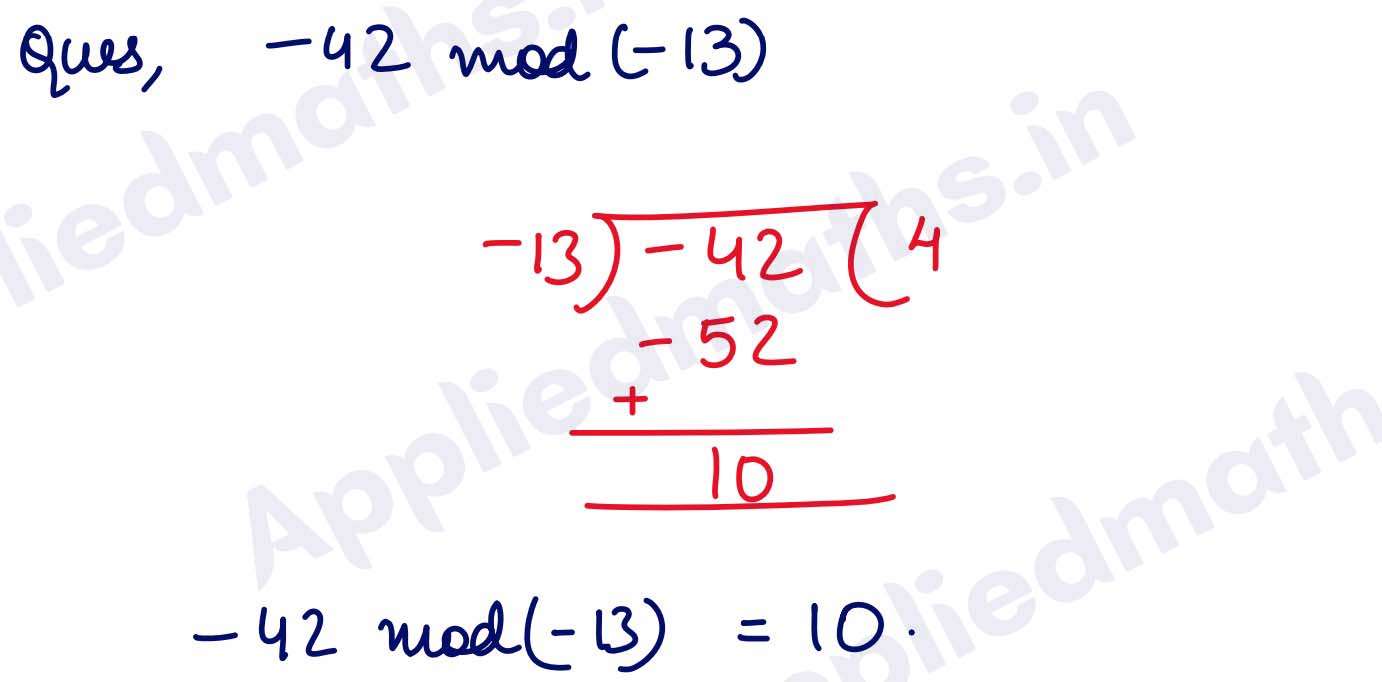
Q1. 25 mod 2
Solution :

Q2. -8 mod 5
Solution :
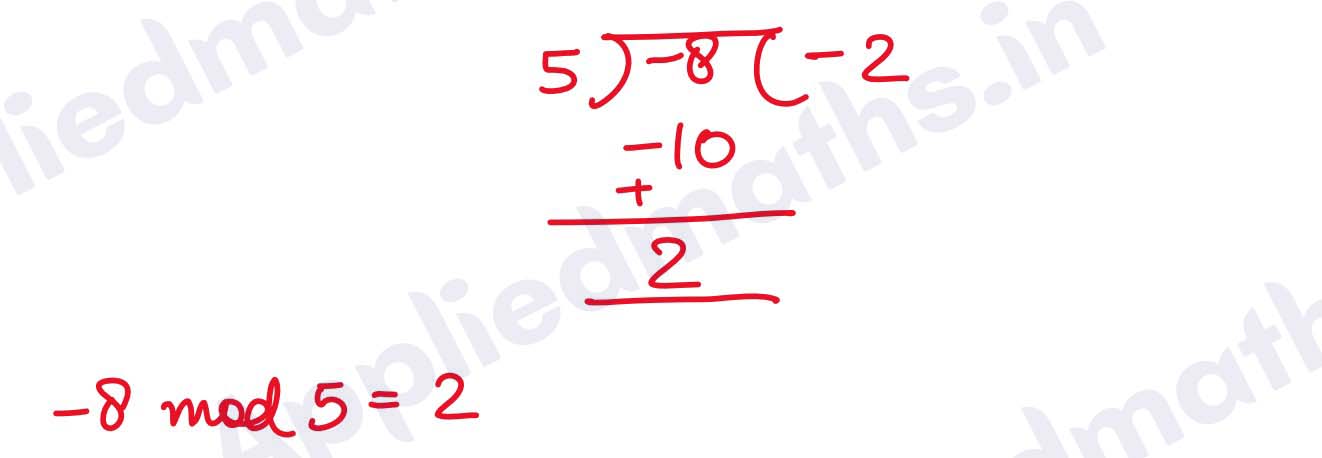
Q3. 42 mod (-13)
Solution :
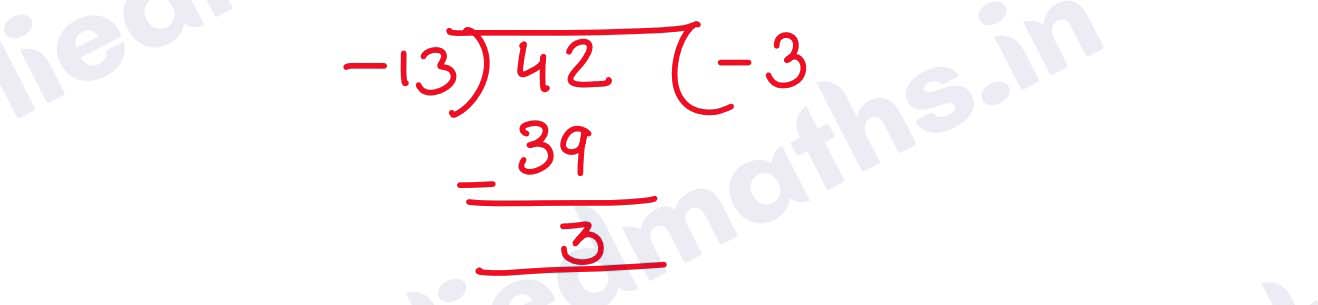
Q4. -42 mod (-13)
Solution :
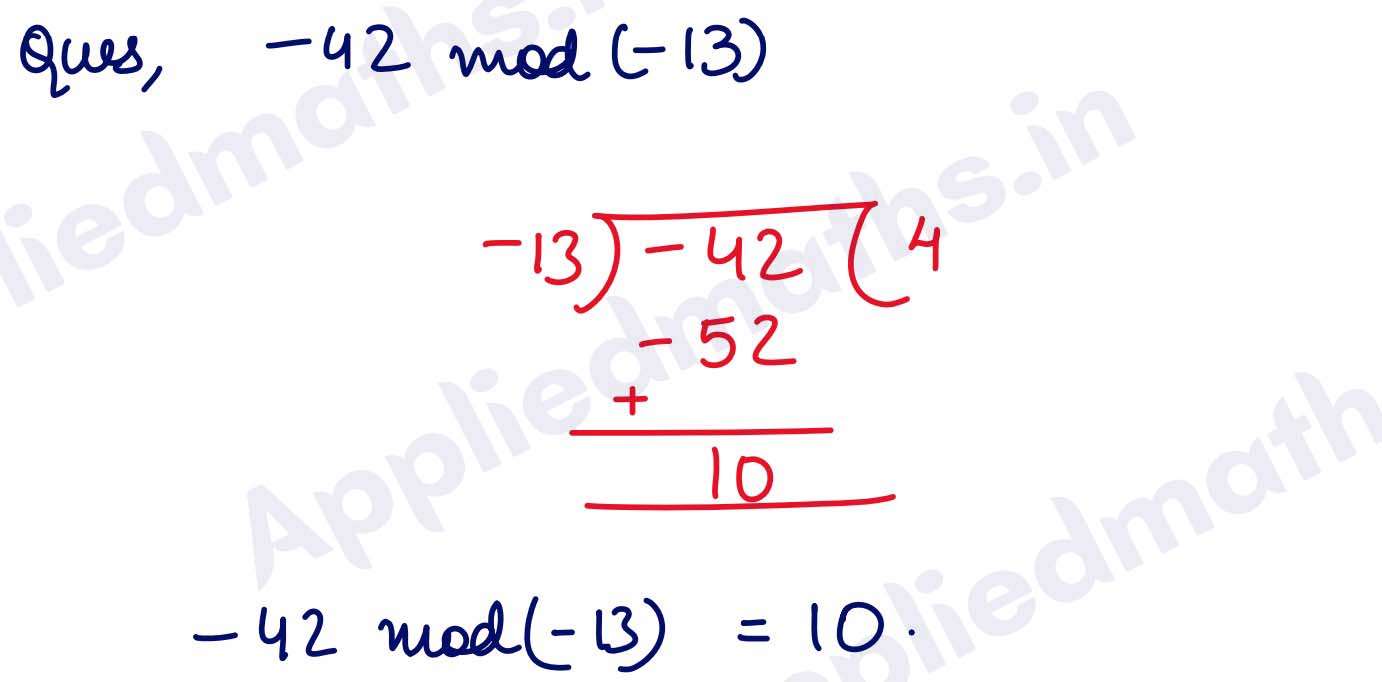
Congruence Modulo :
Let 'a' and 'b' be two integers and n be an integer greater than 1, then a is said to be congruent to b modulo n if n divides the difference of a and b i.e. a ≡ b (mod n) if there exists an integer λ such that a - b = λn.
Properties of Modulo operation :
Addition:
1. If a + b = c then a(mod n) + b(mod n) = c(mod n)
2. If a ≡ b(mod n) then (a + k) ≡ (b + k) mod n, ∀ K ∈ I
3. If a ≡ b(mod n), c ≡ d(mod n) then (a + c) ≡ (b + d)(mod n)
4. If a ≡ b(mod n) then -a ≡ -b(mod n)
Q5. (576 + 789) mod 9
Solution :

Multiplication:
1. If a.b = c then a(mod n) . b(mod n) = c(mod n)
2. If a ≡ b(mod n) then Ka ≡ Kb(mod n)
3. If a ≡ b(mod n), c ≡ d(mod n) then ac = bd(mod n)
Q6. (489 x 813) mod 7
Solution :
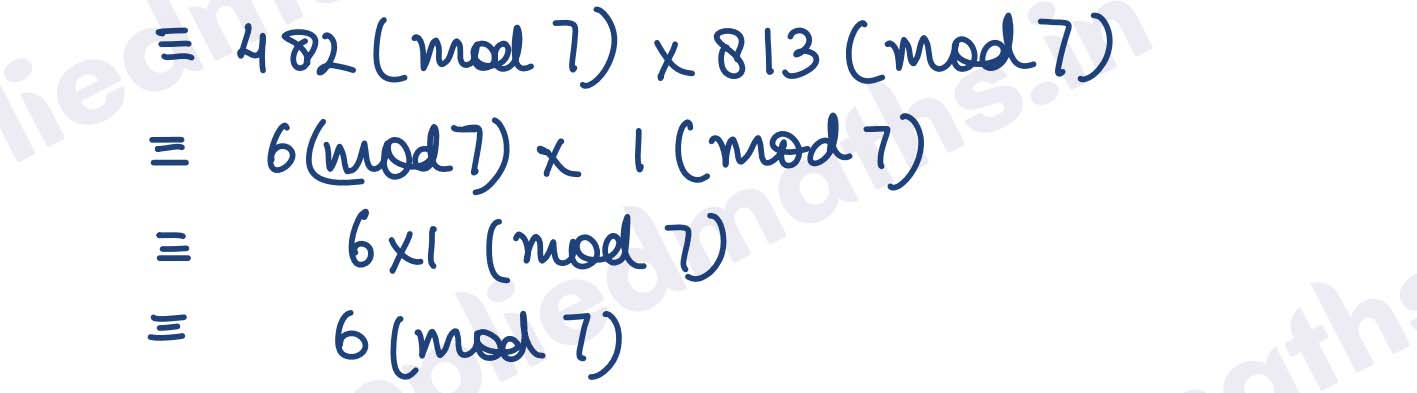

Find last 1/ 2/ 3 digit :
→ For last 1 digit : we take "mod 10"
→ For last 2 digit : we take "mod 100"
→ For last 3 digit : we take "mod 100"
Q7. Find the last digit of 1717
Solution :



Q8. Find the last 2 digit of 2020
Solution :

Addition Modulo :

Q9. Find the Addition modulo 7 if a and b are 12 and 6 respectively.
Solution :

Q10. Find the Addition modulo 17 if a and b are 3 and 11 respectively.
Solution :
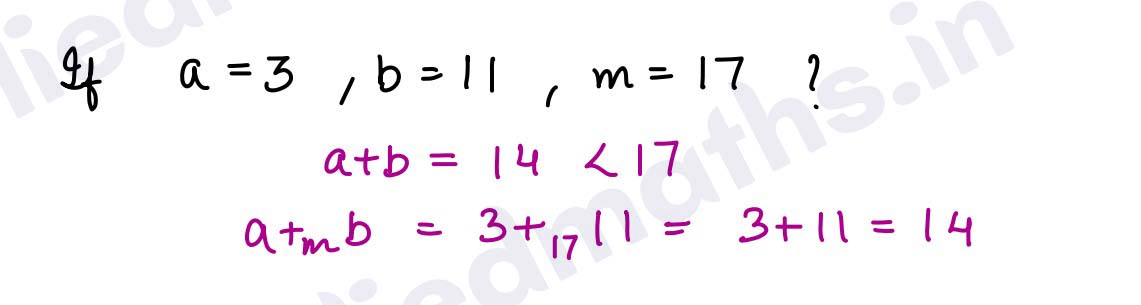
Subtraction Modulo :

Q11. Find the subtraction modulo 8 if a and b are 15 and 4 respectively.
Solution :

Q12. Find the subtraction modulo 12 if a and b are 20 and 12 respectively.
Solution :

Multiplication Modulo :
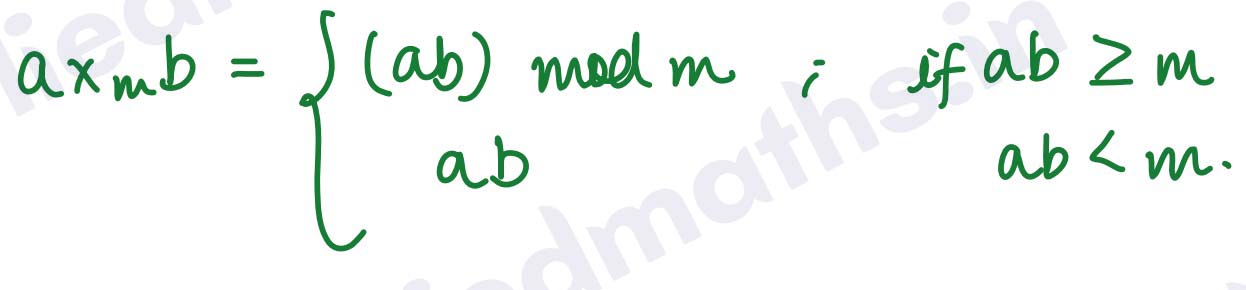
Q13. Find the multiplication modulo 8 if a and b are 5 and 7 respectively.
Solution :
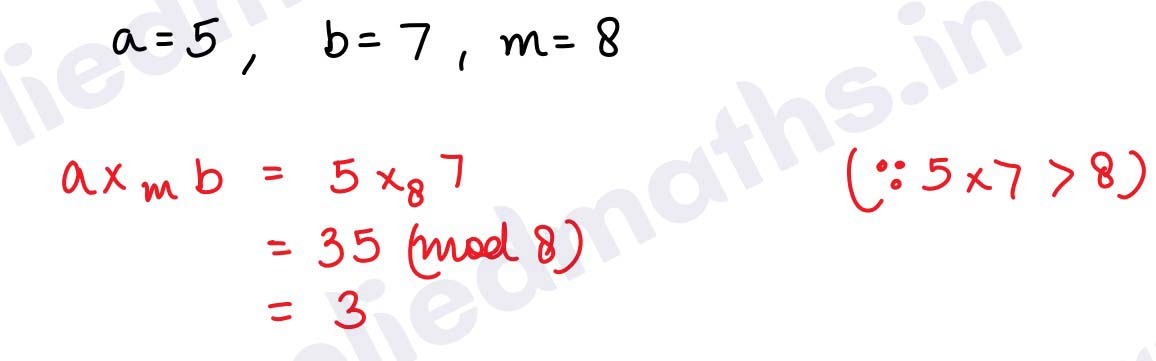
Q14. Find the multiplication modulo 6 if a and b are 2 and 3 respectively.
Solution :
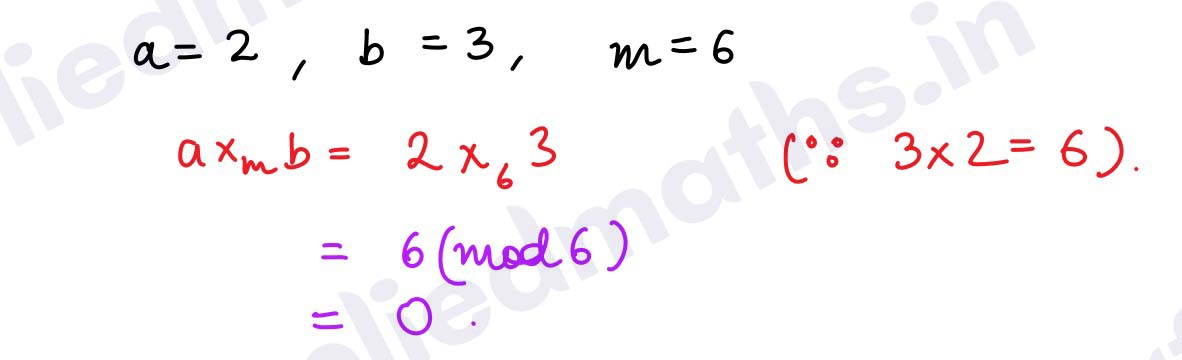
Q15. Find the multiplication modulo 6 if a and b are 1 and 2 respectively.
Solution :