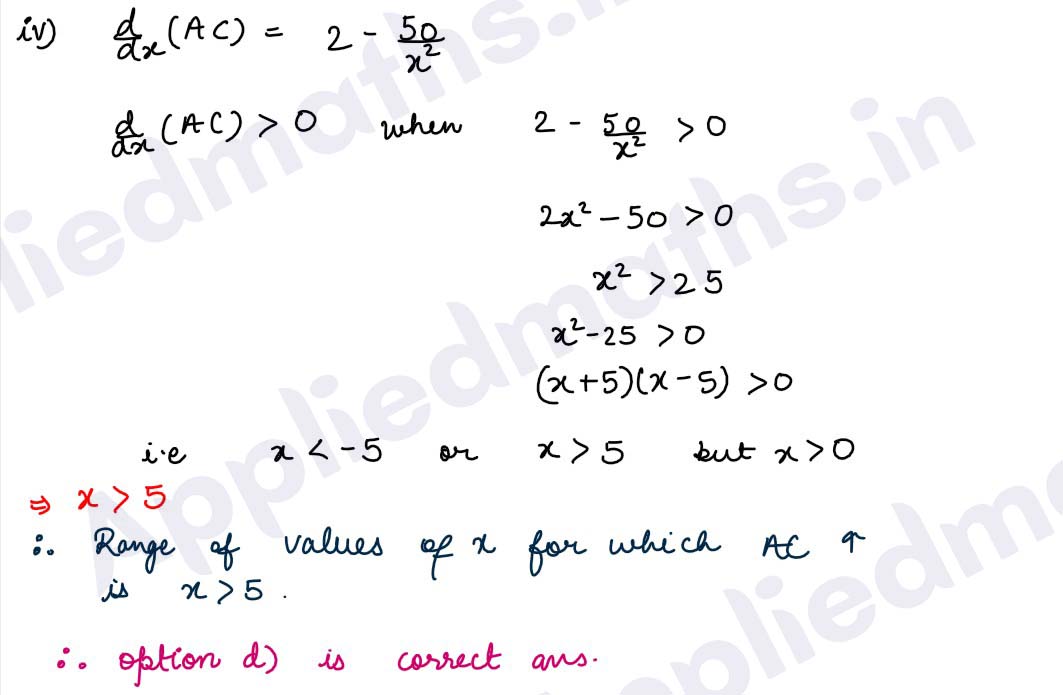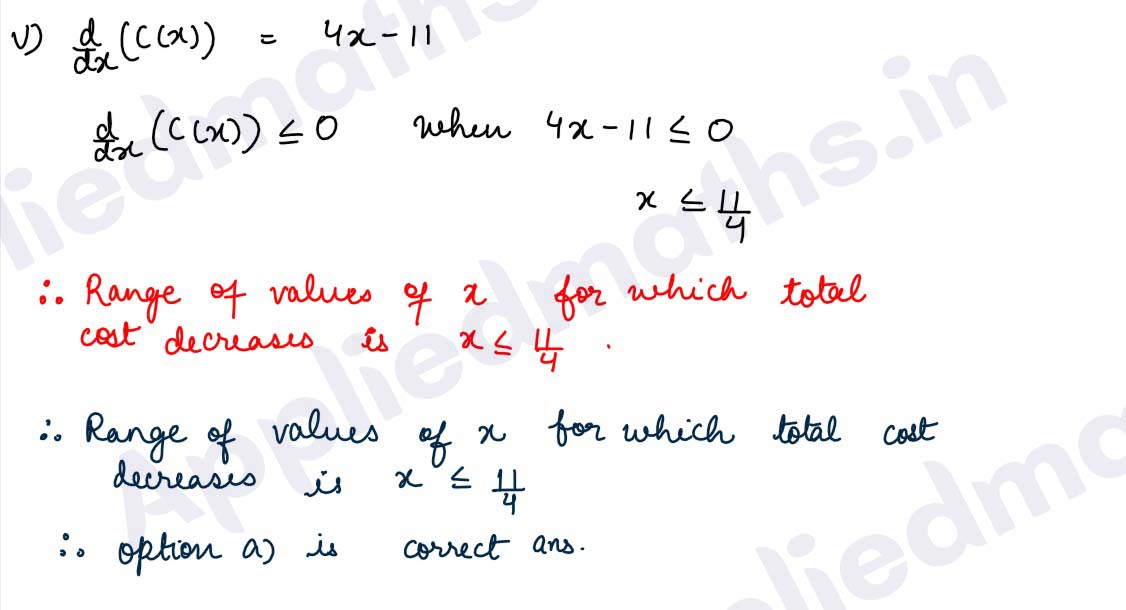Class 12 CBSE Applied Maths Application Of Derivatives Case Study

Class 12 CBSE A.O.D Case Study

Class 12 CBSE Applied Maths aims to develop an understanding of basic mathematical and statistical tools and their applications in the field of commerce (business/ finance/economics) and social sciences. Topics covered in Class 12th Applied Maths includes : Numbers, Quantification and Numerical Applications, Algebra, Calculus, Probability Distributions , Inferential Statistics, Index Numbers and Time-based data , Financial Mathematics , Linear Programming.

Please Select

Case-study-1

A Political Party placed an order to a screen printer for the printing of Party's slogan on a rectangular cloth sheets. A margin of 2.5 cm along length and 1 cm along width of cloth was left. The pictorial view of the slogan in shown below:

If the total area of cloth is 640 cm2, based on the above information, answer the following questions:

(i) The length and the breadth (in cm) of the rectangular part on which the slogan is printed respectively are

(a)x-2.5, y-1
(b) x-5,y-2
(c) x-2,y-5
(d) x-5,y-1

(ii) The relation between x and y is

(a) (x-2.5)(y-1)=640
(b) (x-5)(y-2)=640
(c) xy=640
(d) (x-2)(y-5)=

(iii) Area 'A' of cloth on which slogan matter was written is given by

(a) 650-2x-3200/x
(b) 650+2x+ 3200/x
(c) 600-2x-3200/x
(d) 600 +2x + 3200/x

(iv) What is the value of x for which the printing area is maximum?

(a) 16 cm
(b) 40 cm
(c) 14 cm
(d) 11 cm

(v) What is the value of 'A' when printing of slogan is done on maximum area?

(a) 640 cm²
(b) 418 cm²
(c) 490 cm²
(d) none of these

Solution :

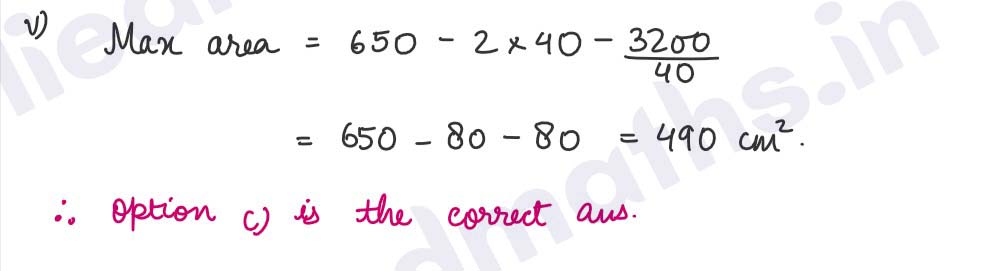
Case-study-2

Saloni has a piece of tin rectangular in shape as shown in the diagram given below. She is going to cut squares from each corners and fold up the sides to form an open box.

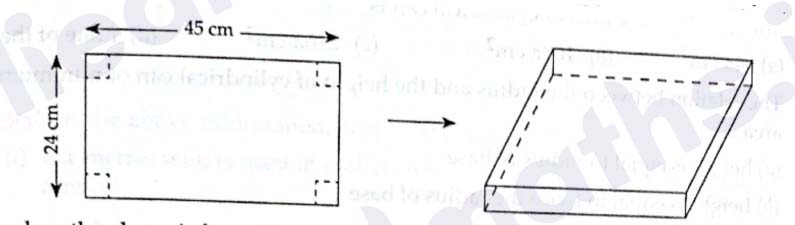
Based on the above information, answer the following questions:
(i) If x is the side of square cut off from each corner of the sheet, then what is the length of open box?

(a) 45-x
(b) 45-2x
(c) 45 +2x
(d) none of these

(ii) What is width of open box?

(a) 24-x
(b) 24+ x
(c) 24-2x
(d) none of these

(iii) Volume 'V' of open box is given by

(a) V = (45-x)(24-x) x
(b) V=(45+x)(24+x) x
(c) V=(45+2x) (24+2x) x
(d) V=(45-2x)(24-2x) x

(iv) What should be the side of square to be cut off so that the volume of box is maximum?

(a) 18 cm
(b) 5 cm
(c) both (a) and (b)
(d) none of these

(v) The maximum value of V (in cm³) is

(a) 5400
(b) 4200
(c) 3600
(d) 2450

Solution :

Case-study-3

A company is planning to launch a new product and decides to pack the new product in closed right circular cylindrical cans of volume 432 πcm³. The cans are to be made from tin sheet. The company tried different options.

Based on the above information, answer the following questions:

(i) If 7 cm is the radius of the base of the cylinder and h cm is height, then

(a) rh=216
(b) r(r+h)=216
(c) rh² = 432
(d) r²h=432

(ii) If S cm² is the surface area of the closed cylindrical can, then

(a) S= 2π (r²+432/r)
(b) S= π (r²+864/r)
(c) S= π (r²+432/r)
(d) S= 432π/r

(iii) For S to be minimum r is equal to

(a) 3 cm
(b) 6 cm
(c) 8 cm
(d) 12 cm

(iv) Minimum surface area of cylindrical can is

(a) 54 πcm²
(b) 108 πcm²
(c) 216 πcm²
(d) none of these

(v) The relation between the radius and the height of cylindrical area is

(a) height is equal to radius of base
(b) height is equal to twice the radius of base
(c) radius is equal to twice the height
(d) radius is two-third of the height.

Solution :

Case-study-4

A factory owner wants to construct a tank with rectangular base and rectangular sides, open at the top, so that its depth is 2 m and capacity is 8 m³. The building of the tank costs ₹250 per square metre for the base and ₹180 per square metre for the sides.

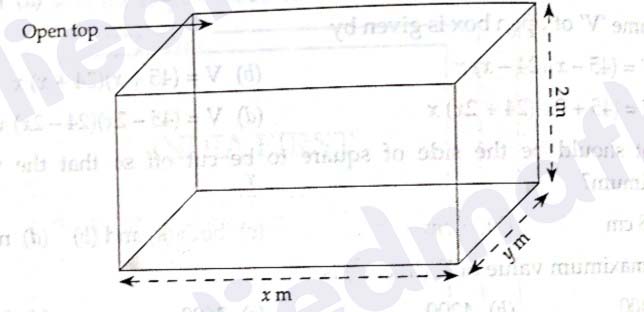
Based on the above information, answer the following questions: (i) If the length and the breadth of the rectangular base of the tank are x metres and mimiy metres respectively, then the relation between x and y is

(a)x+y=4
(b) xy=4
(c) xy=8
(d) xy+x+y=4

(ii) The cost of construction of the sides of the tank is

(a) ₹180 (x+y) (b) ₹360 (x+y) (c) ₹720 (x + y) (d) ₹1120 (x+y)

(iii) If C (in ₹) is the cost of construction of the tank, then C as a function of x is

(d) C= 1120 + 720 (x+4/x)
(b) C=720+1120 (x+4/x)
(c) C=1120+360 (x+4/x)
(d) C=1120+180 (x+4/x)

(iv) The cost of construction of the tank is least when the value of x is

(a) 1
(b) 3 /2
(c) 2
(d) 3

(v) The least cost of construction of the tank is

(a) ₹2000
(b) ₹3000
(c)₹3600
(d) ₹4000

Solution :

Case-study-5

A carpenter has a wire of length 28 m. He wants to cut into two pieces, one of the two pieces is to be made into a square and other into a circle.

Based on the above information, answer the following questions:

(i)If x metres wire is used in making a square, then what is the expression of combined area A?

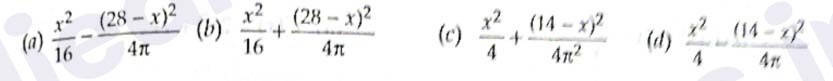
(ii) What is the length of radius for minimum combined area?

(a) 28/π+4
(b) 112/π+4
(c) 14/π+4
(d) none of these

(iii) What is the length of circular part?

(a) 28/π+4
(b) 14/π+4
(c) 14π/π+4
(d) 28π/π+4

(iv) What is the length of square part?

(a) 112/π+4
(b) 112π/π+4
(c) 14π/π+4
(d) 28/π+4

(v) The minimum combined area of square and circle is

(a) 196/π+4 m²
(b) 196/(π+4)² m²
(c) 196/π-4 m²
(d) none of these

Solution :

Case-study-6

A firm has the cost function C(x)=x³/3-7x²+ 111x +50 and demand function x = 100-p.

Based on the above information, answer the following questions:

(i) The total revenue function is

(a) R(x) = x²-100x
(b) R(x) = 100x-x²
(c) R(x) = 100-x
(d) none of these

(ii) The total profit function is

(a)-x³/3 +6x²-11x-50
(b)-x³/3-6x²-11x+50
(c)x³/3+6x²-11x+50
(d) -x³/3-6x²-11x+50

(iii) The value of x for which profit is maximum is

(a) 8
(b) 9
(c) 10
(d) 11

(iv) The maximum profit is

(a) ₹133.11
(b) ₹113.31
(c) ₹111.33
(d) ₹133.11

(b) The marginal revenue when x = 10 units is

(a) 900
(b) 80
(c) 90
(d) 800

Solution :

Case-study-7

The average cost function associated with producing and marketing x units of an item is given by 50

AC=2x-11 + 50/x

Based on the above information, answer the following questions:

(i) The total cost function is

(a) C(x)=2x²-11x+50
(b) C(x)=2- 50/x²
(c) C(x)=2x- 50/x
(d) C(x)=2x²+11x-50

(ii) The marginal cost function is

(a) MC=4x+ 11
(b) MC=4x-11
(c) MC = 2 + 50/x²
(d) MC= 100/x³

(iii) The marginal cost when x = 4 units is

(a) ₹5
(b) ₹27
(c) ₹18
(d) ₹13

(iv) The range of values of x for which AC is increasing is

(a) x< 5
(b) x>-5
(c) x<-5
(d) x>5

(v) The range of values of x for which total cost is decreasing is

(a) x ≤ 11/4
(b) x ≥ 11/4
(c) x<- 11/4
(d) x>-11/4

Solution :

Contact Us