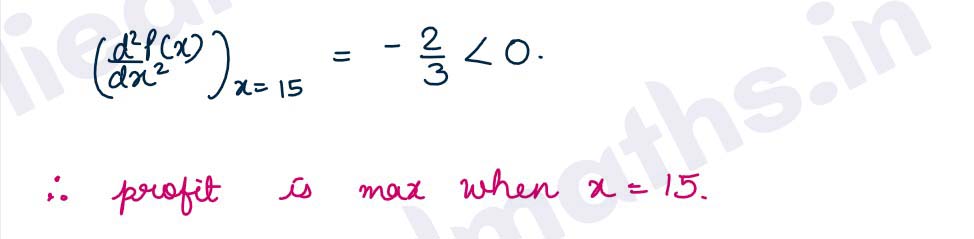Class 12 CBSE A.O.D Exercise 6.10
Class 12 CBSE Applied Maths aims to develop an understanding of basic
mathematical and statistical tools and their
applications in the field of commerce (business/ finance/economics) and social
sciences. Topics covered in Class 12th Applied Maths includes : Numbers, Quantification and
Numerical Applications, Algebra, Calculus, Probability Distributions , Inferential Statistics, Index
Numbers and Time-based data , Financial Mathematics , Linear Programming.
Please Select
Q1. Given the total cost function for x units of a commodity as
C(x) = 1/3 x3 + 3x²-16x+2. Find
(i) the marginal cost function
(ii) the average cost function.
Solution :

Q2. The cost function C(x) of a firm is given by C(x) = 2x²-4x+ 5. Find
(i) the average cost, and
(ii) the marginal cost when x = 10.
Solution :

Q3. The total cost function for a production is given by C(x) = 3/4 x2-7x+27. Find the number of units produced for which M.C. = A.C.
Solution :


Q4. he average cost function for x units of a commodity is
AC=1/3x2+3x-7+ 16/x
(i) Find the marginal cost.
(ii) Show that the marginal average cost is given by x (MC)-C(x)/x2
Solution :


Q5. Verify that d/dx (AC) = 1/x (MC-AC) for
(i) C(x) = √ax+b+c
(ii) C(x)= 5x2/√x2+3 +600.
Solution :



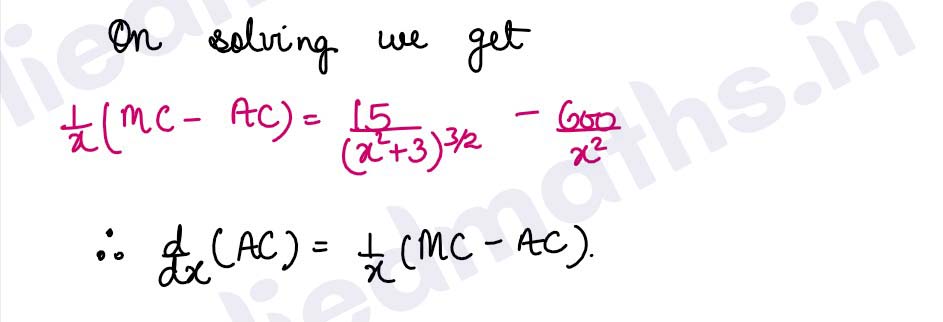
Q6. The total variable cost of manufacturing x units in a firm is ₹ (3x+x5/25). Show that the average variable cost increases with output x.
Solution :

Q7. If C= 2x (x+4/x+1) is the total cost of production of x units of a commodity, show that marginal cost falls continuously as x increases.
Solution :

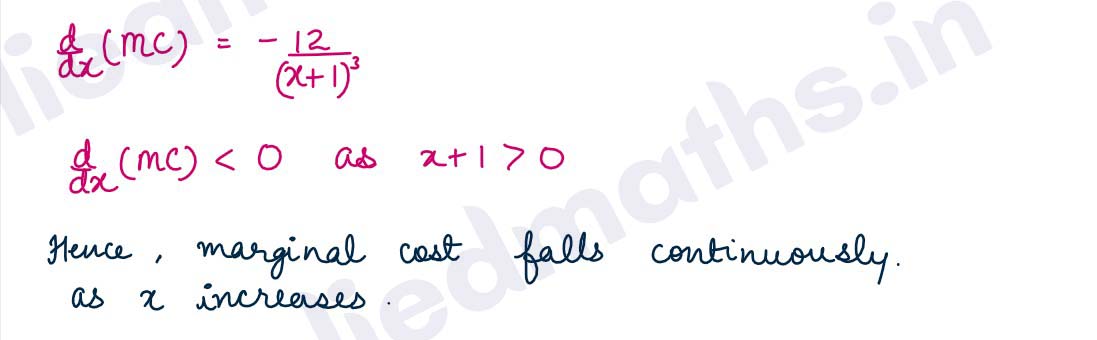
Q8. The average cost function AC for a commodity is given by AC = x + 5 + 36/x in
terms of
output x. Find
(i) the total cost and the marginal cost as the functions of x.
(ii) the output for which AC increases.
Solution :


Q9. If C= ax2 + bx+k is the total cost function, find
(i) slope of average cost function (AC function).
(ii) slope of marginal cost function (MC function).
Solution :

Q10. The demand function of a monopolist is given by p= 1500-2x-x2. Find the marginal revenue for any level of output x. Also, find the marginal revenue (MR) when x = 10
Solution :

Q11. The demand for a certain product is represented by the equation
p=300+25x-12 (in rupees)
(i) Find the marginal revenue function.
(ii) Obtain the marginal revenue when x = 12 units and interpret it.
(ii) Calculate R(13)-R(12) and interpret it.
Solution :


Q12. The total revenue in rupees received from the sale of x units of a product is
given by
R(x)=300x- x2/5 .Find
(i) the average revenue
(ii) the marginal revenue
(iii) the total revenue when MR = 0.
Solution :
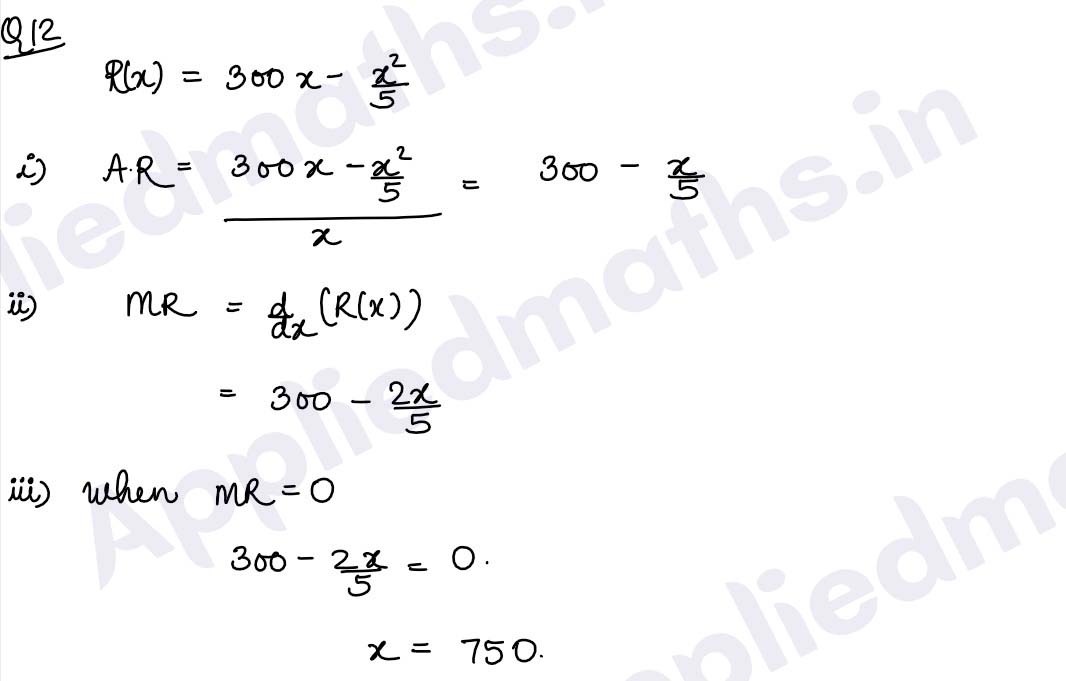

Q13.If p= 100/q+2 -4 represents the demand function for a product where p is the price per unit when q units are sold, find the marginal revenue
Solution :

Q14.A company finds that total revenue from sale of q units of its product is 2q rupees wheras the cost is 500+ 1/2(q/20)2 .Find the rate of change of profit when q= 500.
Solution :

Q15.Given the total cost function for x units of a commodity as
C(x)=1/3 x3 + x2-8x +5, find:
(i) the marginal cost function
(ii) average cost function
(iii) slope of average cost function.
Solution :

Q16.If the cost of production of x units is C(x)=40-20x + 10x2, find the average cost function and the output x where average cost is minimum. Verify that the average cost is equal to the marginal cost at this level of output.
Solution :



Q17.The demand function of a monopolist is p(x) = 300-x2. Find
(i) the
revenue
function
(ii) the marginal revenue function
(iii) the output x when revenue is maximum.
Solution :


Q18.If the demand function is given by x = 600-p/8 , where the price is ₹p per unit and the manufacturer produces x units per week at the total cost of ₹(x²+78x+2500), find the valer of x for which the profit is maximum
Solution :


Q19.A product can be manufactured at a total cost C(x)=x2/100+100x+40,where x is the number of units produced. The price at which each unit can be sold is given by p(x)=200-x/400. Determine the production level x at which the profit is maximum. What is the price per unit and total profit at this level of production?
Solution :


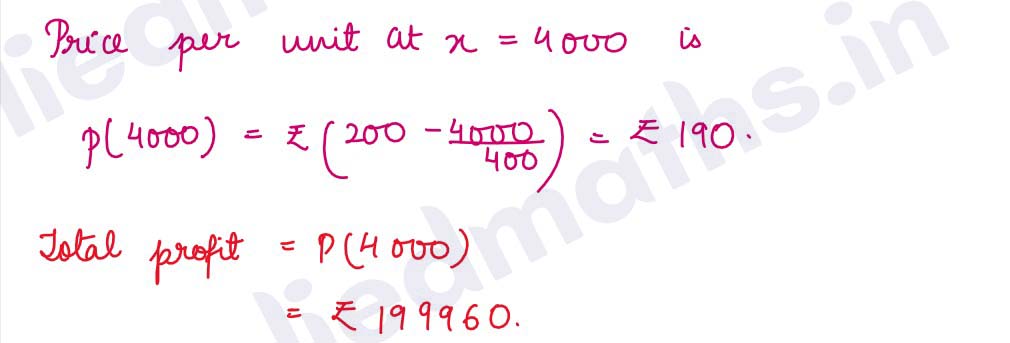
Q20.A manufacturer can produce x items at a total cost of ₹(120x+ x2/2).If he sells the whole produce at ₹p per item, where p = 2(100-x/4), then find the production level x at which the profit is maximum. What is the price per item and the total profit?
Solution :

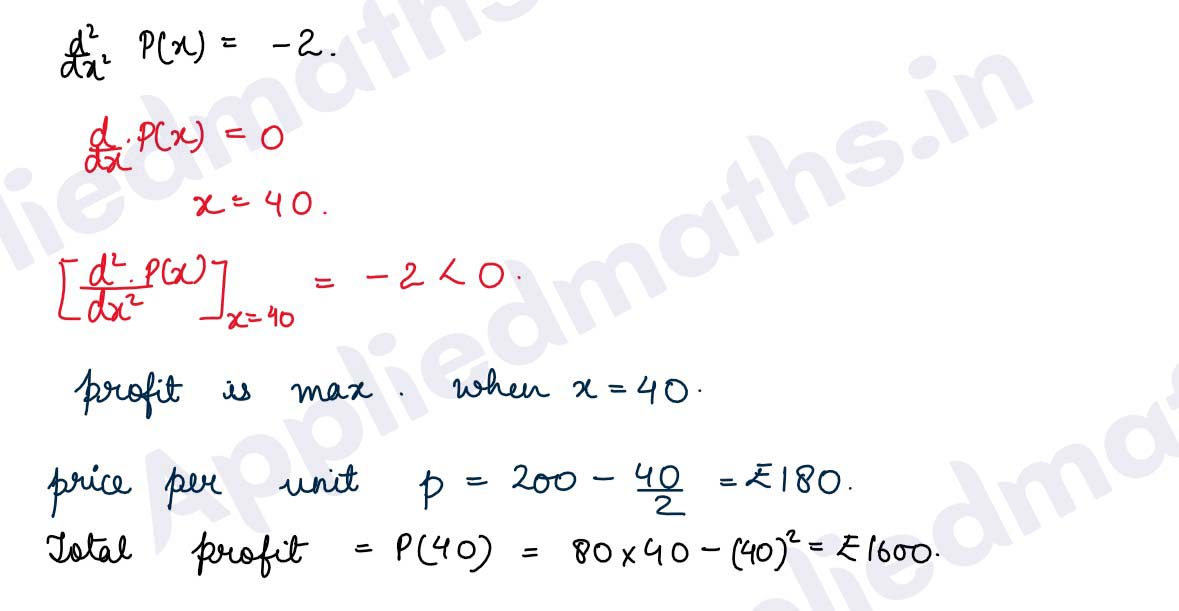
Q21.Find the profit maximising output level, given x = 200 — 10p and AC = 10 + 7/30x where x represents the units of output, p is the price per unit and AC is the average cost.
Solution :