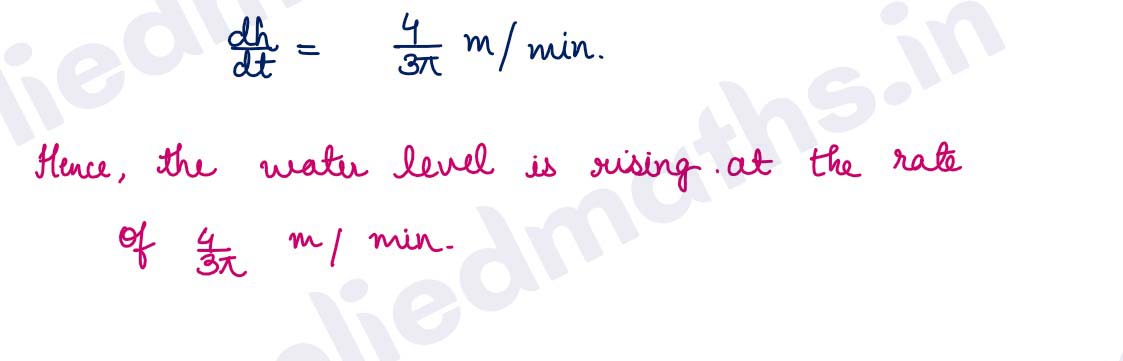Class 12 CBSE A.O.D Exercise 6.1
Class 12 CBSE Applied Maths aims to develop an understanding of basic
mathematical and statistical tools and their
applications in the field of commerce (business/ finance/economics) and social
sciences. Topics covered in Class 12th Applied Maths includes : Numbers, Quantification and
Numerical Applications, Algebra, Calculus, Probability Distributions , Inferential Statistics, Index
Numbers and Time-based data , Financial Mathematics , Linear Programming.
Please Select
Q1. Find the rate of change of the area of a circle concerning its radius when the radius is 6 cm.
Solution :

Q2. If the radius of a circle is increasing at the rate of 0.7 cm/sec, at what rate is its circumference increasing?
Solution :

Q3. If the radius of a circle is increasing at the rate of 3 cm/sec, at what rate is its area when its radius is 10 cm?
Solution :

Q4. If the sides of a square are decreasing at the rate of 1.5 cm/sec, at what rate is its perimeter decreasing?
Solution :

Q5. If the sides of a square are decreasing at the rate of 1.5 cm/sec, at what rate is its area decreasing when its side is 8 cm?
Solution :

Q6. Find the rate of change of the volume of a cube with respect to its edge when the edge is 5 cm.
Solution :

Q7. If an edge of a variable cube is increasing at the rate of 3 cm/sec, at what rate is its volume increasing when its edge is 10 cm?
Solution :
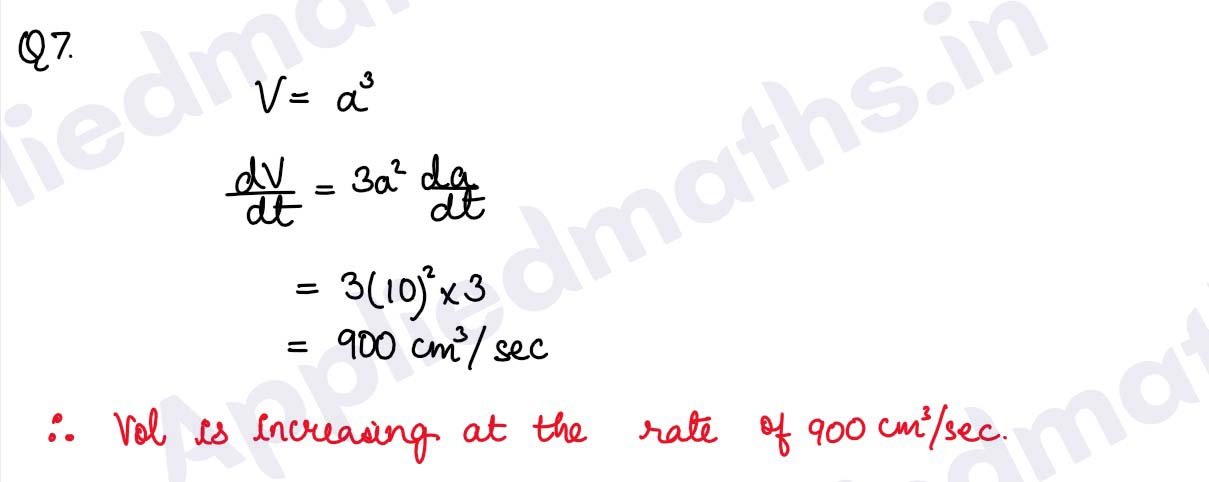
Q8. A balloon which always remains spherical has a variable radius. Find the rate at which its volume is increasing with respect to radius when the radius is 10 cm.
Solution :

Q9. If the radius of a balloon which always remains spherical is increasing at the rate 1.5 cm/sec, at what rate is its surface area increasing when its radius is 12 cm?
Solution :

Q10. If the radius of a soap bubble is increasing at the rate 1/2 of cm/sec, at what rate is its volume increasing when the radius is 1 cm?
Solution :

Q11. A cylindrical tank of radius 10 m is being filled with wheat at the rate of 314 cubic metre per hour. Find the rate at which the depth of the wheat is increasing, take л = 3.14.
Solution :

Q12. Find the rate of change of the whole surface of a closed circular cylinder of radius r and height h with respect to change in radius.
Solution :

Q13. A stone is dropped into a quiet lake and waves move in circles at the speed of 5 cm/sec. At the instant when the radius of the circular wave is 8 cm, how fast is the enclosed area increasing?
Solution :

Q14. The length x of a rectangle is decreasing at the rate of 5 cm/minute and the
width y is increasing at the rate of 4 cm/minute. When x = 8 cm and y = 6 cm, find the rate of
change of:
(i) the perimeter
(ii) the area of the rectangle.
Solution :


Q15. The volume of a cube is increasing at the rate of 9 cubic centimetres per second. How fast is the surface area increasing when the length of the edge is 10 centimetres?
Solution :
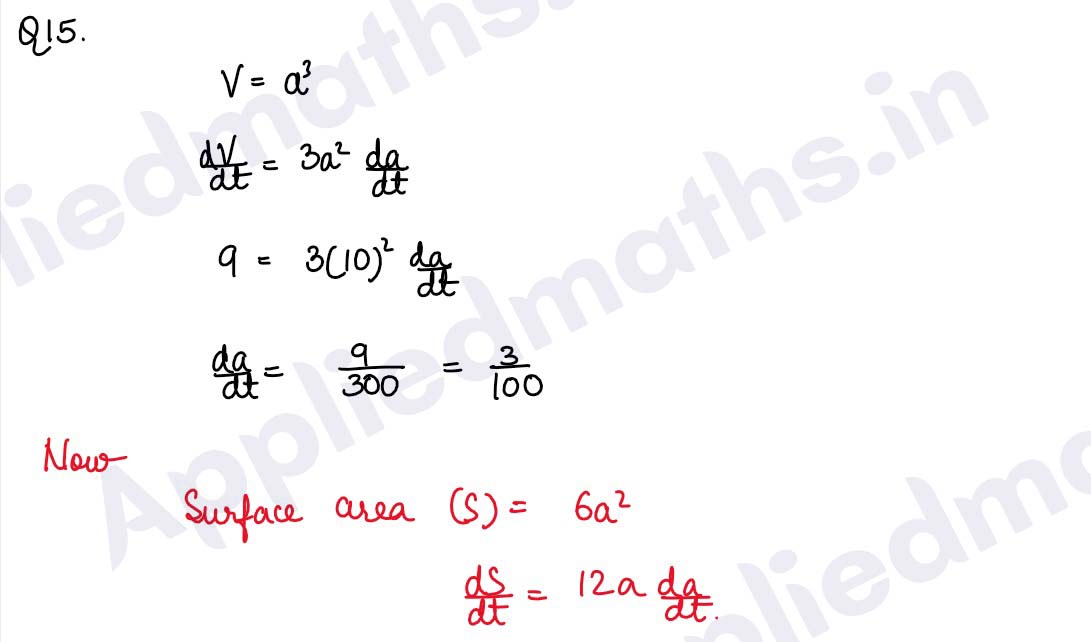

Q16. A particle moves along the curve y = 2/3x^3 + 1. Find the points on the curve at which the y-coordinate is changing twice as fast as the x-coordinate.
Solution :

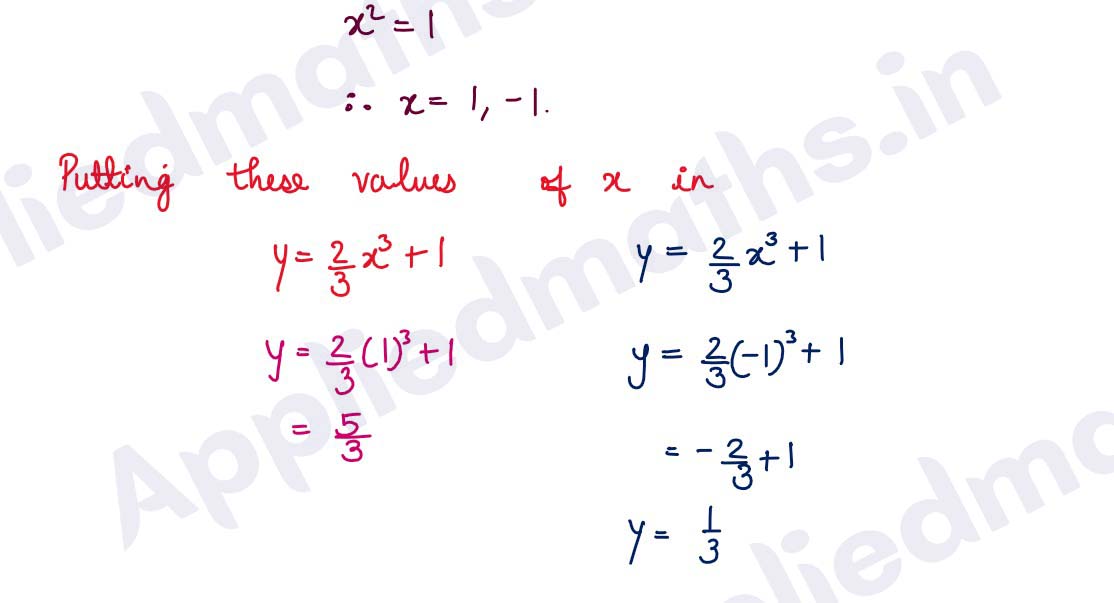
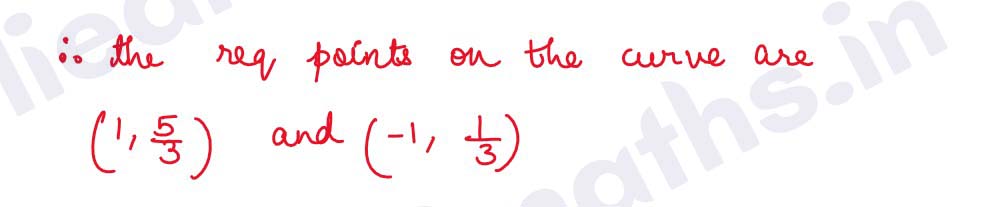
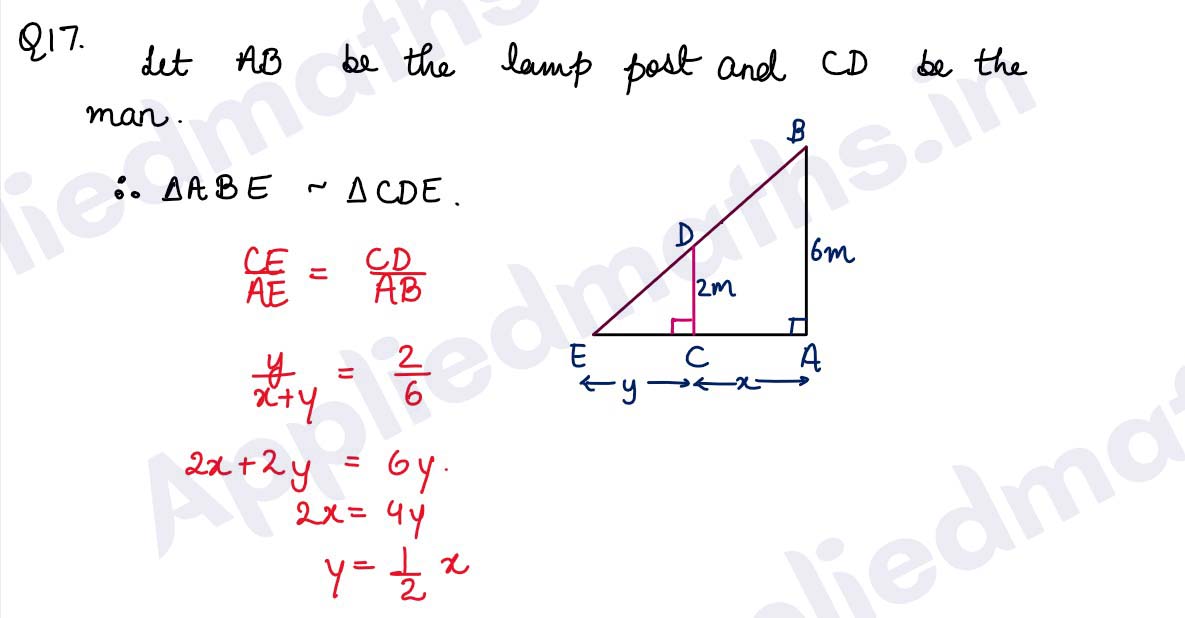
Q17. A man of height 2 metres walks at a uniform speed of 5 km/h away from a lamp post which is 6 metres high. Find the rate at which the length of shadow increases.
Solution :

Q18. A kite is 120 m high and 130 m of string is out. If the kite is moving horizontally at the rate of 5.2 m/sec, find the rate at which the string is being paid out at that instant.
Solution :

Q19. Sand is poured from a pipe at the rate of 12 cm3/sec. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4 cm?
Solution :


Q20. A conical vessel whose height is 4 metres and of base radius 2 metres is being filled with water at the rate of 0.75 cubic metres per minute. Find the rate at which the level of the water is rising when the depth of water is 1.5 metres.
Solution :