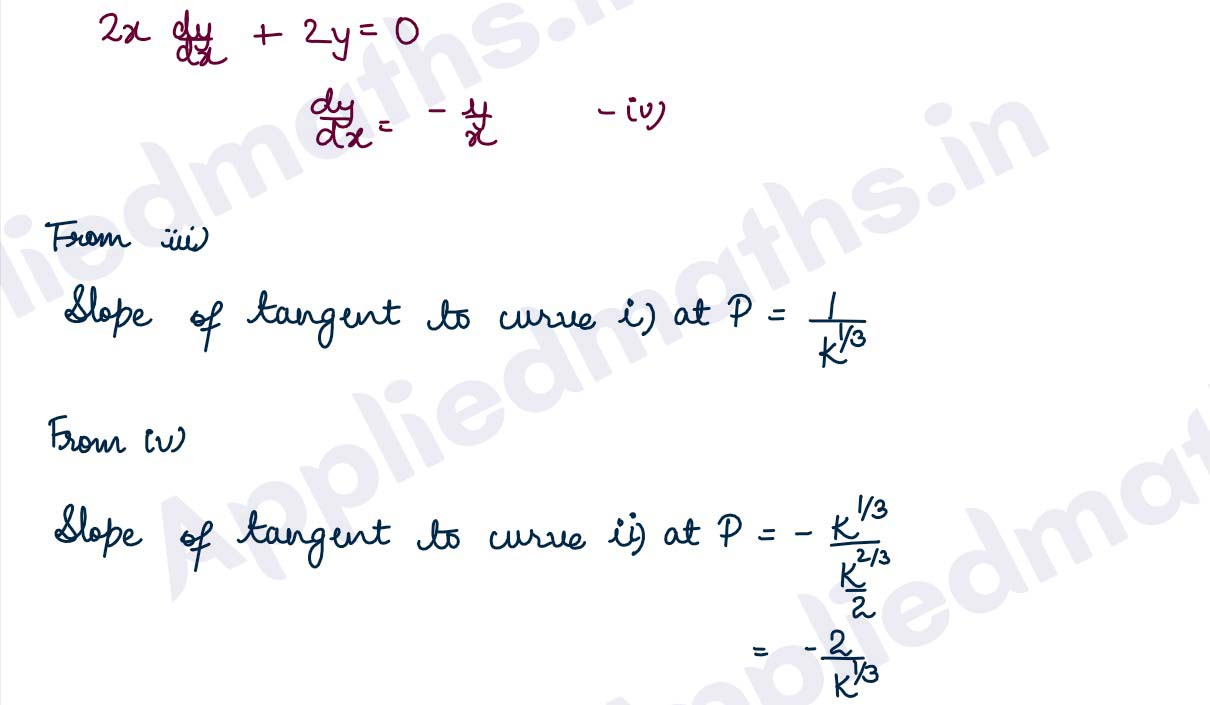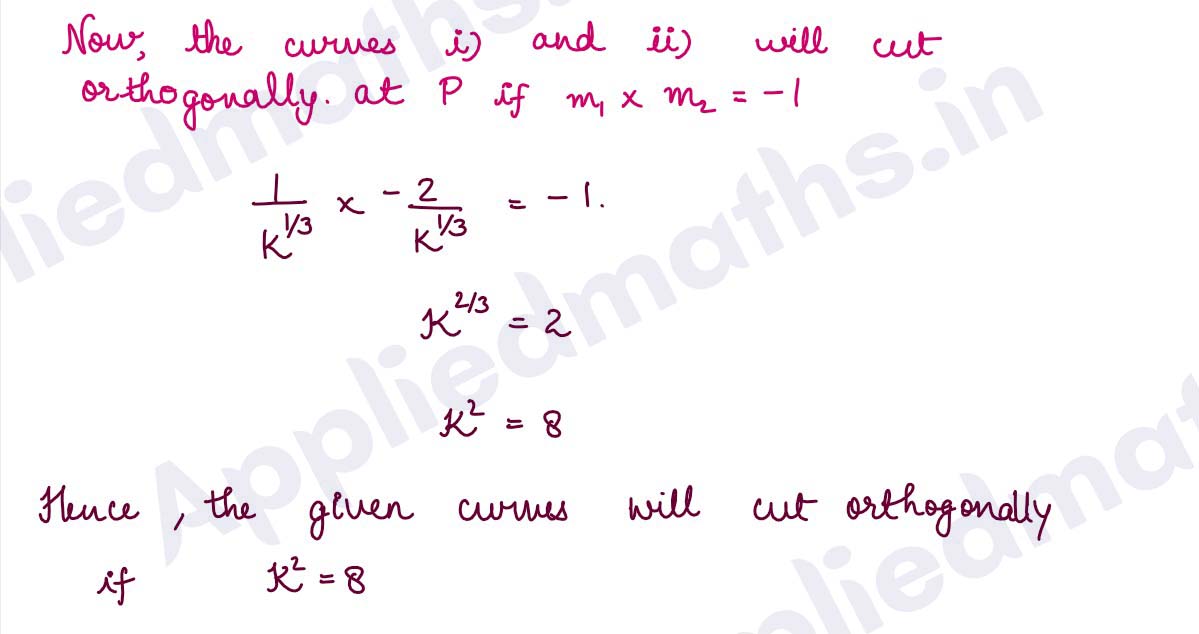Class 12 CBSE A.O.D Exercise 6.2
Class 12 CBSE Applied Maths aims to develop an understanding of basic
mathematical and statistical tools and their
applications in the field of commerce (business/ finance/economics) and social
sciences. Topics covered in Class 12th Applied Maths includes : Numbers, Quantification and
Numerical Applications, Algebra, Calculus, Probability Distributions , Inferential Statistics, Index
Numbers and Time-based data , Financial Mathematics , Linear Programming.
Please Select
Q1. What is the slope of the tangent to the following curves:
(i) y = 3x^4 – 4x , at x = 4?
(ii) x^2 + 3y + y^2 = 5 , at the point (1, 1)?
(iii) y=x^3 – 3x + 2 at the point whose x-coordinate is 3?
Solution :



Q2. What is the slope of the normal to the following curves:
(i) y = x^3 – 5x^2 – x + 1 at the point (1,-4)?
(ii) y = 2x^2 + 3e^x at x = 0?
Solution :


Q3. Find the point on the curve y = x^2 – 2x + 3 at which the tangent is parallel to x-axis.
Solution :


Q4. Find the slope of the tangent to the curve y = (x – 1)/(x – 2) at x = 10.
Solution :

Q5. Show that the tangents to the curve y = 7x^3+ 11 at the points where x = 2 and x = -2 are parallel.
Solution :

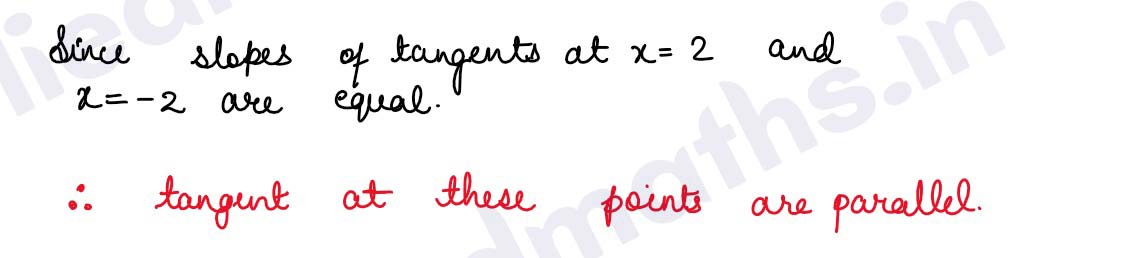
Q6. Find the points on the curve x^2/4 + y^2/25 = 1 at which the tangents are
(a) parallel to x-axis
(b) parallel to y-axis.
Solution :




Q7. Find the points on the curve y=x^3 – 3x^2 + 2x at which the tangent lines are parallel to the line y-2x+3=0.
Solution :


Q8. Find the equations of the tangent and the normal to each of the following
curves
at the given point:
(i) y = x3 at (1, 1)
(ii) y=x4-6×3+13×2 – 10x + 5 at (1, 3)
(iii) y=x4-6×3+
13×2-10x + 5 at (0,5)
(iv) y = x2 at (0,0)
Solution :


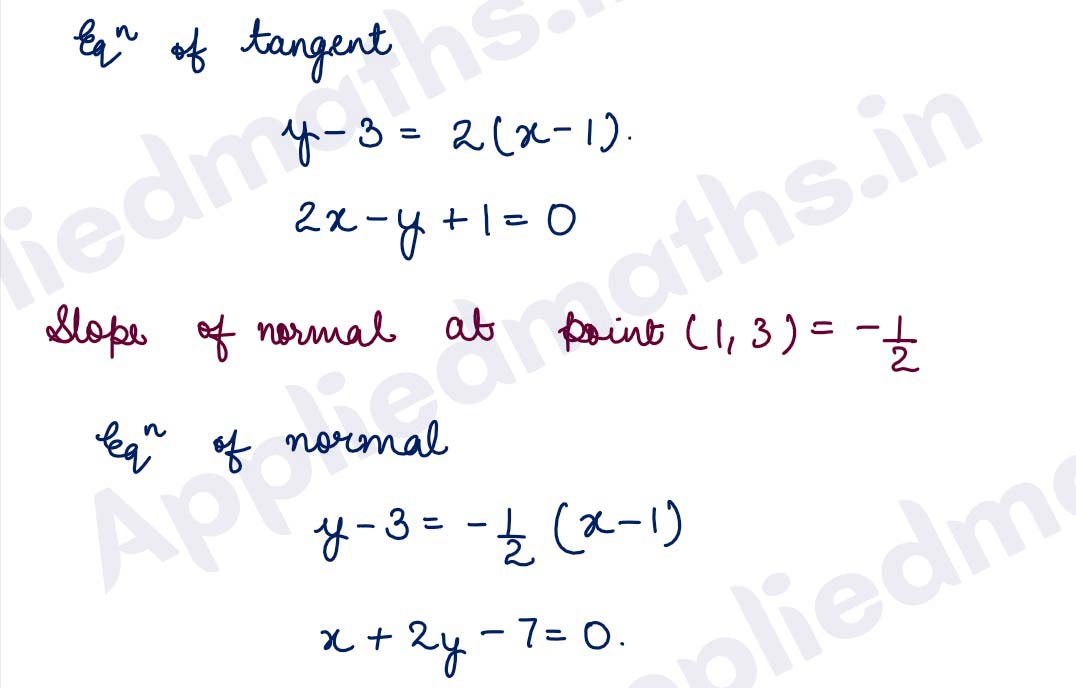

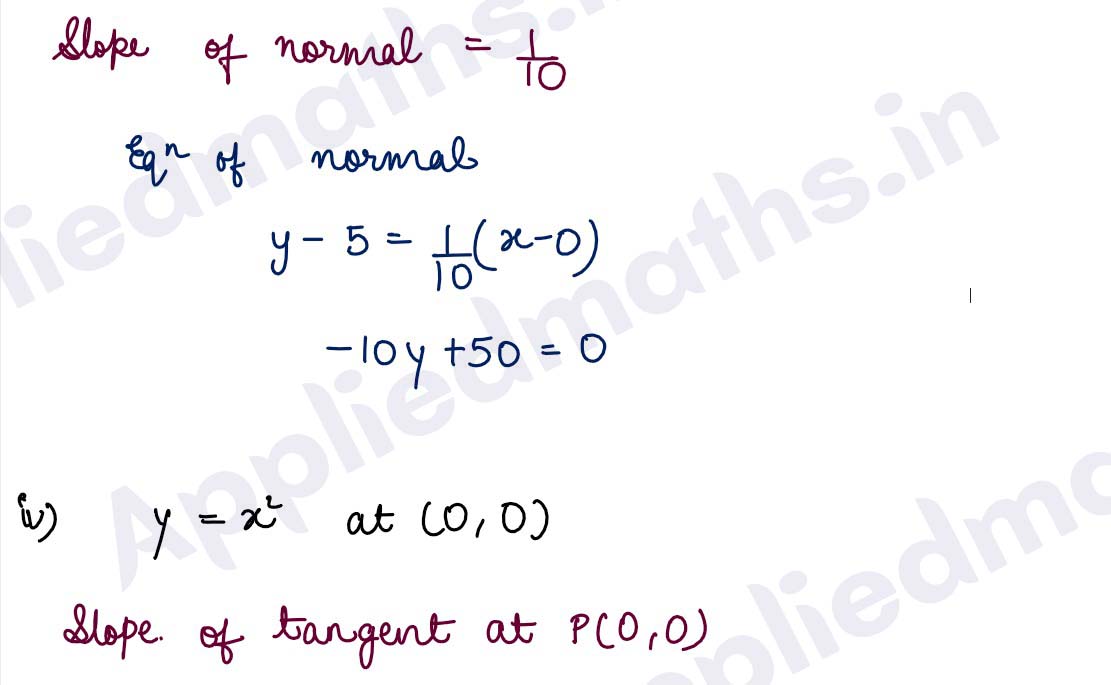

Q9. Find the equation of the normal to the curve ay^2 = x^3 at the point (am^2, am^3).
Solution :


Q10.Find the equations of the tangent and the normal to the curve x^2/3 + y^2/3 = 2 at (1, 1).
Solution :

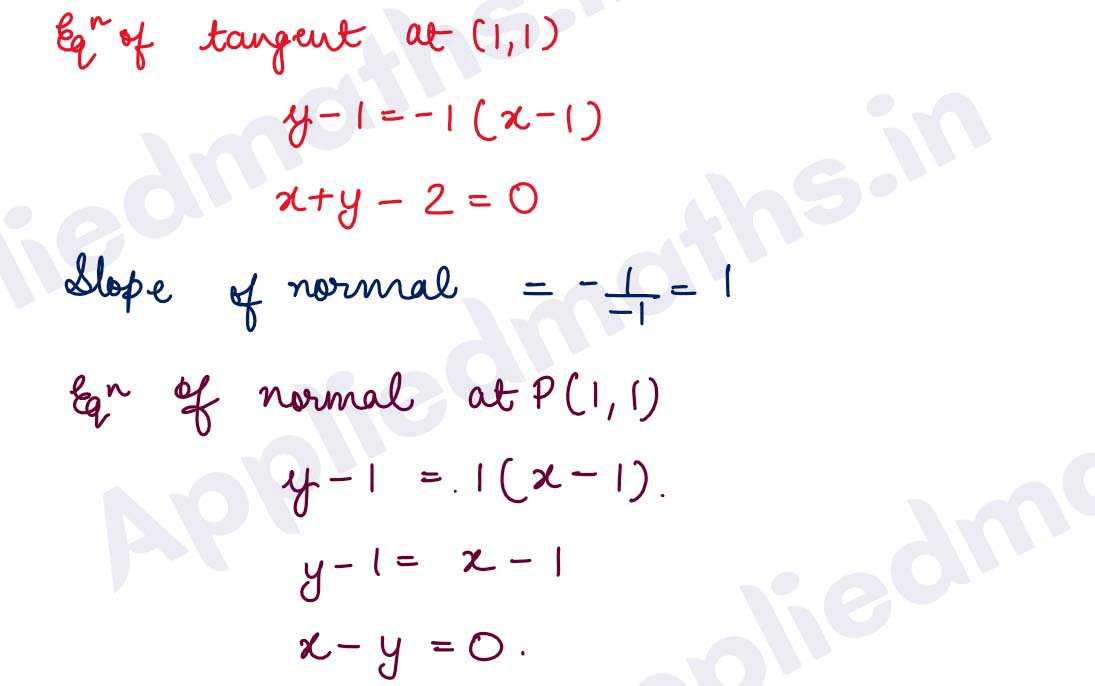
Q11. Find the equations of all lines having slope 2 and being tangents to the curve y + 2/(x-3) = 0.
Solution :
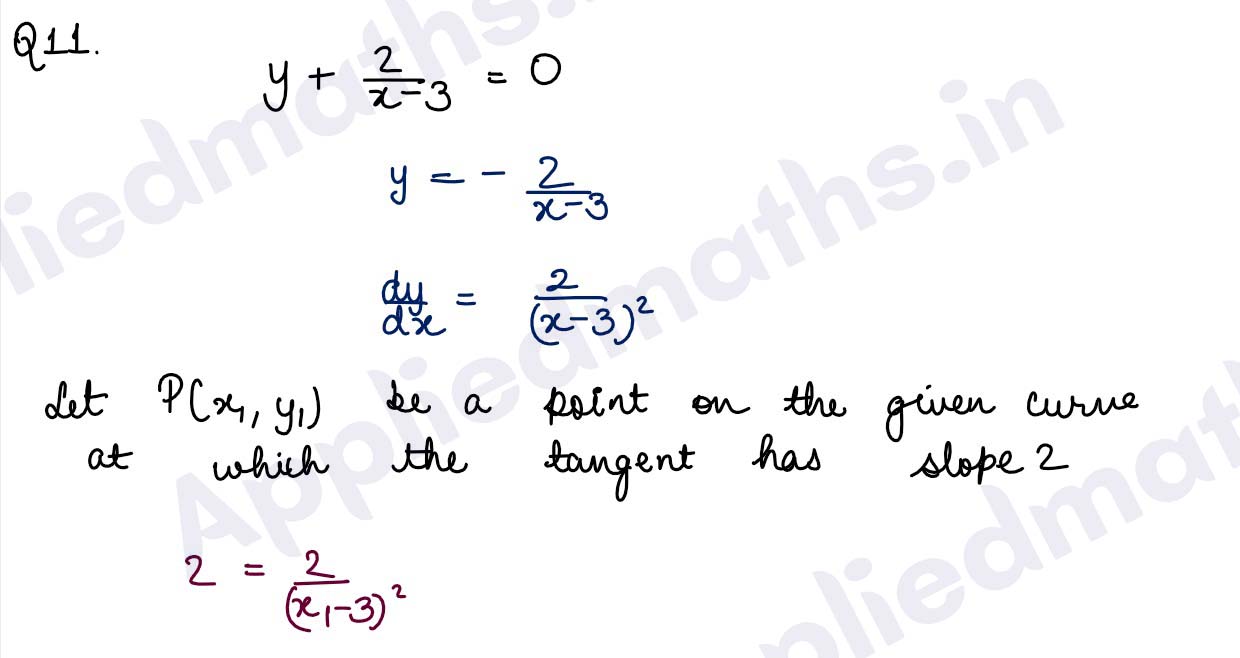

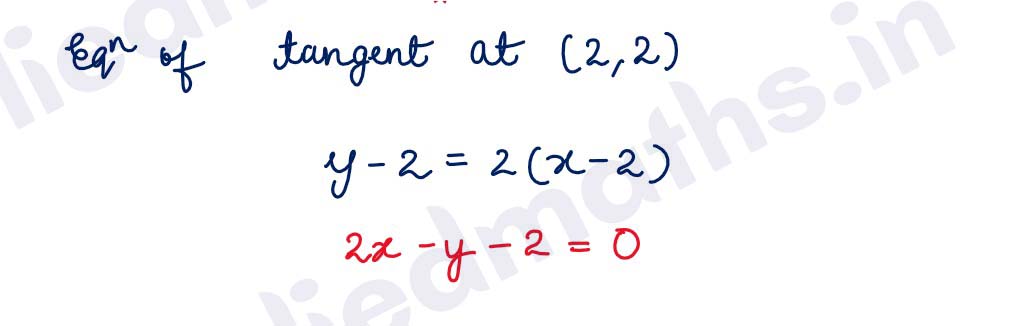
Q12. Find the equations of the normals to the curve 3x^2 – y^2 = 8 which are parallel to the line x + 3y=4.
Solution :



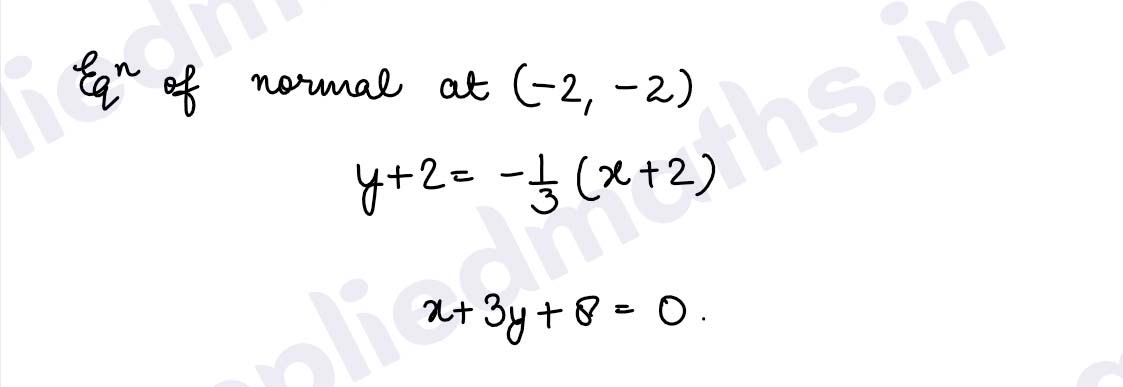
Q13 Find the equation of the normal to the curve y = x + 1/x, x > 0, perpendicular to the line 3x – 4y = 7.
Solution :
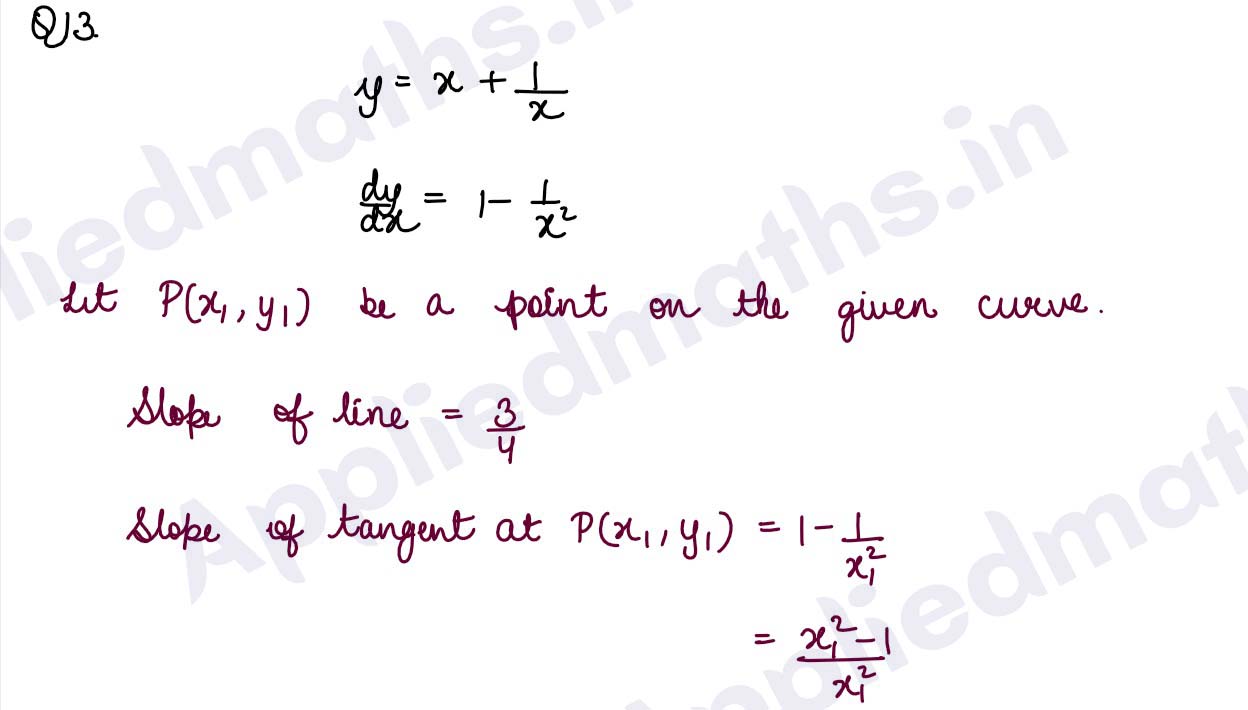

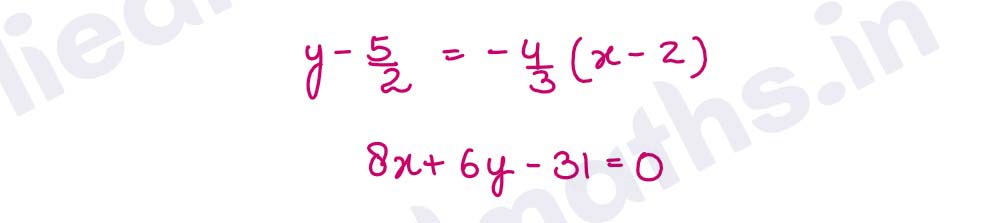
Q14. Find the equation of the normal to the curve x^2 = 4y which passes through the point (-1,4).
Solution :

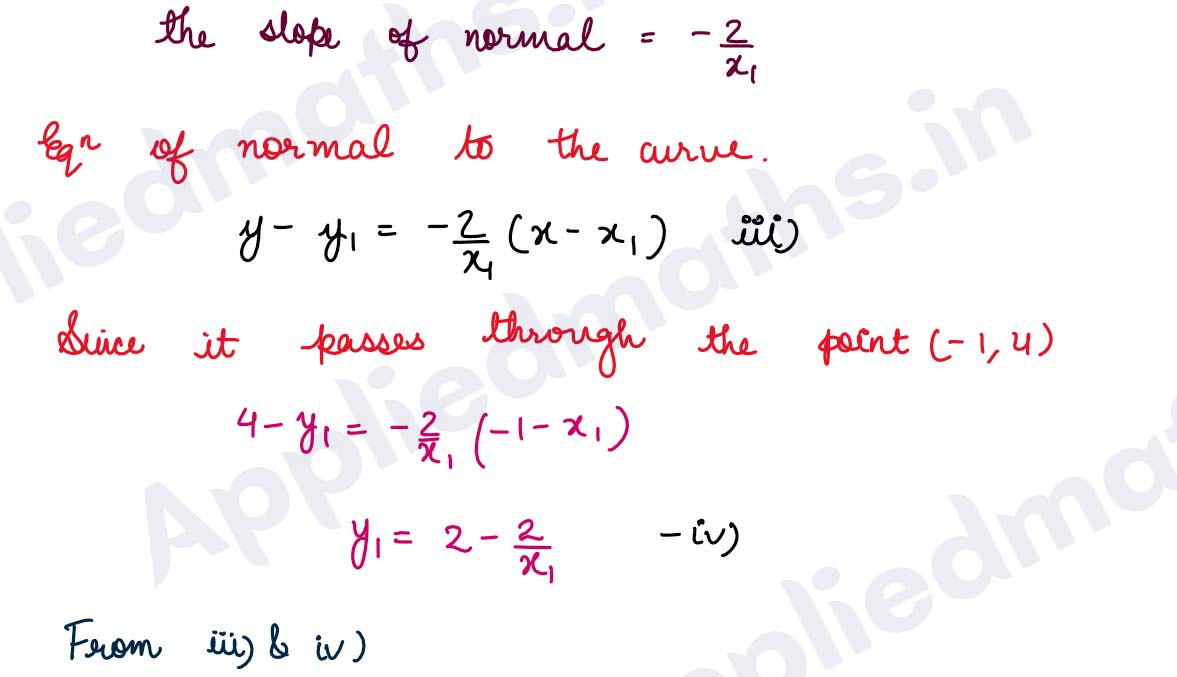
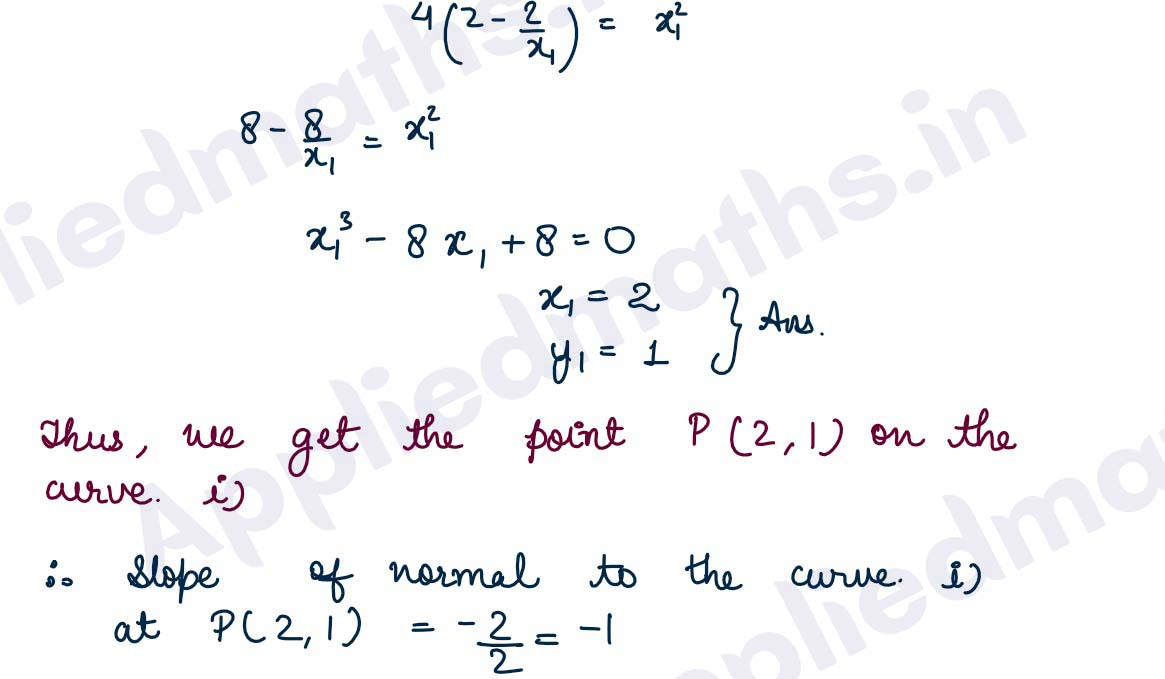
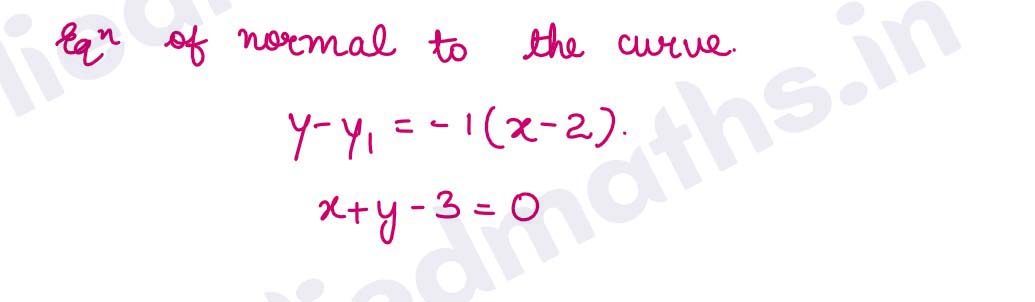
Q15. WProve that the curves xy = 4 and x^2 + y^2 = 8 touch each other.
Solution :


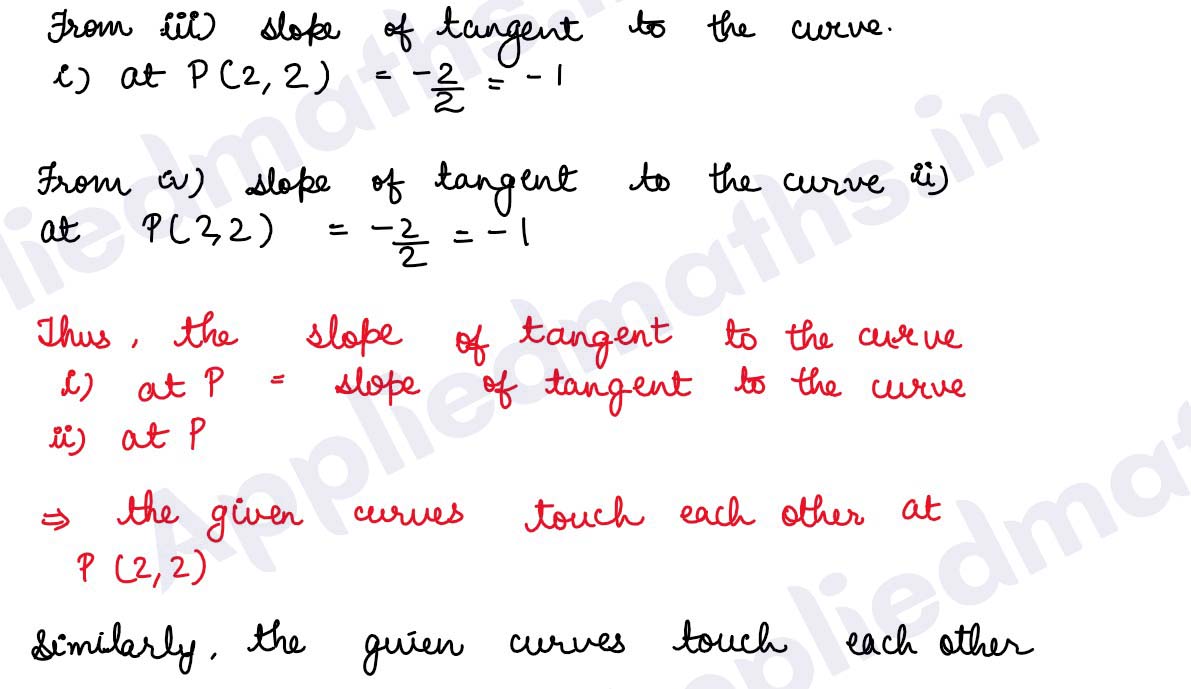
Q16. Find the condition that the curves 2x = y2 and 2xy = k intersect orthogonally.
Solution :